Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 82
O aparato da Figura 4-60 é chamado de máquina de Atwood e é usado para medir a aceleração de queda livre medindo-se a aceleração dos dois blocos ligados pelo fio que passa pela polia. Suponha uma polia sem massa e sem atrito e um dio sem massa. (a) Desenhe o diagrama de corpo livre de cada bloco. (b) Use os diagramas de corpo livre e as leis de Newton para mostrar que a magnitude da aceleração de cada bloco e que a tensão no fio são e . (c) Estas expressões fornecem resultados plausíveis se no limite e no limite ? Explique.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão. A caixa de maior massa vai puxar a de menor massa através da cordinha.
Como solicitado no item (a), está exposto abaixo o diagramde corpo livre dos dois blocos:
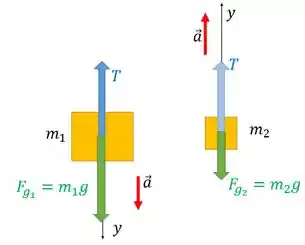
A tensão é a força com que a corda puxa um bloco. Ela é a mesma para os dois e tem a mesma magnetude porque eles estão presos à mesma corda.
Mas como , a força peso do bloco 1 é maior.
É possível notar que em cada bloco foi considerado um sistema de coordenadas diferente, colocando no sentido da aceleração, para facilitar nossos cálculos.
Passo 2
Para resolver o item (b), precisamos achar a expressão da aceleração dos blocos e da tensão .
Aplicando a segunda lei de Newton no bloco de massa temos:
Aplicando a segunda lei de Newton no bloco de massa temos:
Passo 3
Como os blocos estão conectados pela polia simples (os blocos estão conectados por uma mesma corda), temos uma aceleração única para os dois corpos:
Substituindo isso nas equações que temos e :
Somando as duas equações, temos:
Colocando em evidência e isolando:
Chegamos em , falta .
Passo 4
Da equação , temos:
Substituindo nossa expressão de aí:
Multiplicando o termo da direita por em cima e embaixo (ou seja, fazendo o MMC):
Passo 5
Para resolver o item (c), temos que analisar as 3 situações que ele propõe e ver se elas fazem sentido quando aplicadas as equações que a gente achou.
Quando , as equações da aceleração e tensão, encontradas no item a), se tornam:
Estes resultados são esperados, pois, se os blocos têm mesma massa, eles se equilíbram (ou seja, eles ficam parados e ) e a tensão na corda em cada lado é a força peso gerada pela massa do bloco.
Passo 6
Para o limite ele quer dizer que a massa é desprezível em relação a massa . Então vamos fazer nas nossas equações e ver o que acontece:
Esses resultados fazem sentido porque se é desprezível, não há nada segurando o outro lado da corda e impedindo o bloco de massa de cair em queda livre (com aceleração ). E se nada segura o outro lado da corda, não há tensão nessa corda.
Para o limite , vamos considerar que é desprezível em relação a . Então vamos fazer
Aqui acontece a mesma coisa que no caso anterior. Esse menos em é só porque nosso sistema de referência é diferente. Mas esses resultados também indicam que entra em queda livre.
Resposta
a)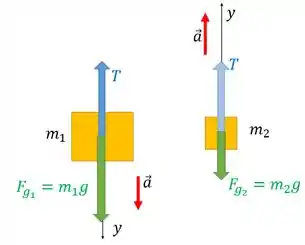 
b) demonstração nos passos
c) resultados são plausíveis, justificação nos passos