Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 57
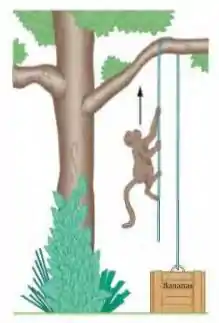
Um macaco de sobe em uma árvore por uma corda de massa desprezível que passa por um galho sem atrito e está presa na outra extremidade a um caixote de , inicialmente em repouso no solo (Fig. 5-54). (a) Qual é o módulo da menor aceleração que o macaco deve ter para levantar o caixote? Se, após o caixote ter sido erguido, o macaco parar de subir e se agarrar à corda, quais são (b) o módulo e (c) o sentido da aceleração do macaco e (d) a tensão da corda?
Passo 1
Esta questão nos dá a massa do macaco (), a massa do caixote (), diz que partem do repouso e nos pede a menos aceleração que o macaco deve ter para levantar o caixote.
Esta é uma questão de aplicação da segunda lei de Newton, portanto, precisamos lembrar que:
Lembrando que esta definição pode ser expandida para as componentes da força.
Passo 2
Vamos iniciar a resolução desta questão aplicando a segunda lei de Newton individualmente para o macaco:
Isolando o :
Passo 3
Em seguida, vamos fazer de maneira análoga para o caixote, porém como ele pede a aceleração mínima, isso ocorrerá quando a tração e o peso se anularem, assim:
Isolando o :
Substituindo esta equação na :
Isolando :
Substituindo os valores conhecidos:
Passo 4
Quando o macaco parar de subir, reescreveremos as equações da segunda lei de Newton:
Isolando na primeira relação:
E substituindo na segunda relação:
Isolando :
Substituindo os valores conhecidos:
Passo 5
Para iniciar a escrever a segunda lei de Newton, eu já escrevi supondo que a o bloco ia descer e o macaco ia subir, porque o bloco é mais pesado do que o macaco. Como, ao calcular a aceleração, nós achamos a aceleração positiva, isso mostra que supomos o sentido correto da aceleração. Caso contrário, o valor encontrado seria negativo.
Portanto, a aceleração do macaco é vertical e para cima.
Passo 6
Para determinar a tensão, podemos substituir os valores na :
Resposta
- ;
- ;
- ;
- .