Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 48
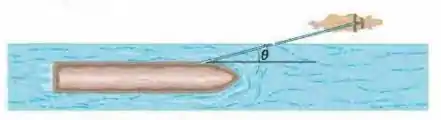
No passado, cavalos eram usados para puxar barcaças em canais, como mostra a Fig. 5-42. Suponha que o cavalo puxa o cabo com uma força de módulo e ângulo em relação à direção do movimento da barcaça, que se desloca no sentido positivo de um eixo . A massa da barcaça é e o módulo da aceleração da barcaça é . Quais são (a) o módulo e (b) a orientação (em relação ao sentido positivo do eixo ) da força exercida pela água sobre a barcaça?
Passo 1
Fala ai galerinha do RespondeAí, tudo beleza? Bora lá fazer esse exercício aqui!
Se liga só, o enunciado nos diz que antigamente se usavam cavalos para puxar a embarcação, onde o barco navegava na agua enquanto que o cavalo puxava o barco pela Terra.
Então suponha que a força que o cavalo exerce é de com um ângulo de em relação ao eixo , o enunciado quer que a gente decubra qual a força que a agua exerce sobre o barco, dado que a aceleração da barcaça é .
Para começar a resolver esta questão precisamos lembrar da definição da segunda lei de Newton:
E lembrar que esta definição pode ser aplicada separadamente para cada componente, eixo por eixo. Assim:
Lembrando que para calcular o módulo do vetor a partir das componentes, usamos a seguinte relação:
E podemos determinar o ângulo em relação ao semieixo positivo:
Este problema nos diz a força de tração na corda (), o ângulo que a tração faz com a horizontal (), a massa da barcaça (), o módulo da aceleração () e nos pede o módulo e a orientação da força exercida pela água sobre a barcaça.
Passo 2
Vamos entender o que está acontecendo fazendo o diagrama de forças
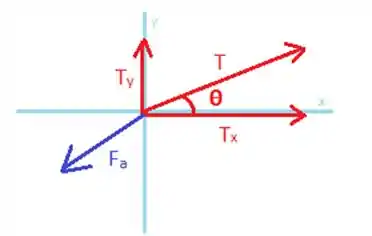
Inicialmente, vamos escrever a segunda lei de Newton para o eixo :
Substituindo os valores conhecidos:
Isolando :
Passo 3
Escrevendo agora a segunda lei de Newton para o eixo :
Como o movimento acontece somente no eixo , . Assim, substituindo os valores conhecidos:
Isolando :
Passo 4
Para determinar o módulo da força da água, usaremos a relação explicitada no passo inicial:
Passo 5
Usaremos a relação dada no passo inicial para determinar o ângulo em relação ao semieixo positivo a partir das componentes:
Como a componente e a componente são negativas e sabendo que o cosseno e o seno são negativos somente no terceiro quadrante, então o valor de nosso ângulo é:
Resposta
- ;
- .