A Fig. 5-58 mostra três blocos ligados por cordas que passam por polias sem atrito. O bloco B está sobre uma mesa sem atrito; as massas são m A = 6,00k g , m B = 8,00k g e m C = 10,0k g . Qual é a tensão da corda da direita quando os blocos são liberados?

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 65

A Fig. 5-58 mostra três blocos ligados por cordas que passam por polias sem atrito. O bloco está sobre uma mesa sem atrito; as massas são , e . Qual é a tensão da corda da direita quando os blocos são liberados?

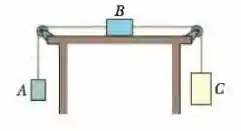
Passo 1

Vamos iniciar fazendo o DCL de cada bloco:

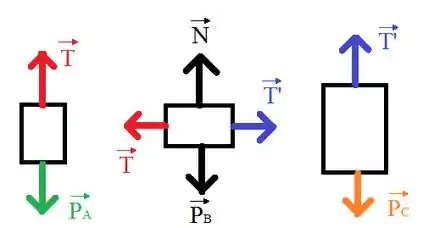
Lembrando que como as polias do problema são ideais, então as trações ilustradas em vermelho têm o mesmo módulo e as trações ilustradas em azul também têm o mesmo módulo.

A partir dessa ilustração, devemos escrever a segunda lei de Newton para a componente dos blocos e e escrever a segunda lei de Newton para a componente do bloco . Lembrando que como os corpos se movem em conjunto a aceleração de todos os são de mesmo módulo. Show? Então vamos começar a escrever as equações:

Como desejamos calcular vamos colocar as outras duas incógnitas do problema e em função de .

Passo 2

Colocando a aceleração em função de na :

Passo 3

Colocando a tensão em função de na :

Na o está em função de e de , então, vamos usar a para colocar o somente em função de :

Passo 4

Por fim, vamos substituir a e a na :

Substituindo os valores conhecidos:

Isolando :

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A aceleração da gravidade g pode ser determinada medindo-se o tempo t que uma massa m 2 leva, em uma máquina de Atwood como a do Problema 82, para cair uma distância L, partindo do repouso. (a) Usando

Se uma das massas da máquina de Atwood da Figura 4-60 é 1,2k g , quanto deve valer a outra massa de forma a que o deslocamento de cada massa, durante o primeiro segundo após a largada, seja 0,30m ? Su

A Figura 4-58 mostra um bloco de 20k g deslizando sobre um bloco de 10k g . Todas as superfícies são sem atrito e a polia é sem atrito e sem massa. Encontre a aceleração de cada bloco e a tensão no fi

Uma pintora de 60k g está sobre uma plataforma de alumínio de 15k g . A plataforma está presa a uma corda que passa através de uma polia acima, o que permite que a pintora eleve a si mesma e a platafo

Um bloco de 20k g , com uma polia presa a ele, desliza ao longo de um trilho sem atrito. Ele está conectado, por um fio sem massa, a um bloco de 5,0k g , como mostra o arranjo da Figura 4-59. Encontre