Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.6 - Ex. 60
Na figura 29-74, uma corrente circula em uma espira formada por dois segmentos radiais e duas semicircunferênciais de raios e com um centro comum . Determine (a) o módulo e (b) o sentido (para dentro ou para fora da página) do campo magnético no ponto P e (c) o módulo e (d) o sentido do momento magnético da espira.
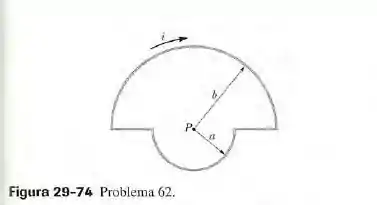
Passo 1
Bom, lá da teoria de campos magnéticos produzidos por correntes, temos a situação de um campo produzido no centro de um arco de circunferência, lembra? Lá a gente encontra a seguinte fórmula para calcular o campo:
Quais informações nós temos para resolver essa questão? Temos a corrente na espira, o raio dela, a corrente que circula e o valor de . Vamos aplicar esses valores na equação para encontrar o valor do campo.
De acordo com a regra da mão direita, o campo aponta para dentro do papel no ponto .
Passo 2
O momento magnético da espira leva em consideração a área dela no cálculo. Para essa configuração de espira, a área é dada por . Assim, o módulo do momento magnético é:
O sentido de é o mesmo de , ou seja, para dentro do papel.
Resposta
- ;
- O campo aponta para dentro do papel no ponto ;
- ;
- O sentido de é o mesmo de , ou seja, para dentro do papel.