Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 3
3. || Um asteróide de 4,0 $ 1010 kg está indo diretamente de encontro
ao centro da Terra a constantes 20 km/s. A fim de salvar o planeta,
os astronautas impulsionam uma gigantesca rocha contra o asteróide
em uma direção perpendicular ao movimento do mesmo. O
foguete usado gera 5,0 $ 109 N de empuxo. O foguete é disparado
quando o asteróide se encontra a 4,0 $ 106 km da Terra. Despreze a
força gravitacional da Terra sobre o asteróide, assim como a rotação
do planeta em torno do Sol.
a. Se a missão falhar, quantas horas levará até que o asteróide atinja
a Terra?
b. O raio aproximado da Terra é de 6.400 km. Em que valor mínimo
de ângulo o asteróide deve ser desviado a fim de não atingir a
Terra?
c. O motor do foguete funciona ao máximo durante 300 s antes que
acabe o combustível. A Terra será salva?
Passo 1
Galera o mais importante nesse tipo de exercícios é entender o que esta acontecendo, sempre façam desenhos e tentem entender os movimentos, porque sem isso é muito fácil se confundir e as vezes calcular uma coisa nada a ver com o que esta sendo pedido.
Agora você pode estar pensando, “Como que eu vou desenhar isso?”, “Essa questão não faz sentido”, “De onde ta vindo essa gigantesca rocha?”.
E realmente esse exercício não faz sentido nenhum. Fui dar uma olhadinha no original e não é que tem um errinho não tradução. Tem um baita de um erro!
Olha só como deveria ser o enunciado:
3. || Um asteróide de está indo diretamente de encontro ao centro da Terra a constantes 20 km/s. A fim de salvar o planeta, os astronautas prendem um gigantesco foguete no asteróide em uma direção perpendicular ao movimento do asteróide. O foguete usado gera de empuxo. O foguete é acionado quando o asteróide se encontra a da Terra. Despreze a força gravitacional da Terra sobre o asteróide, assim como a rotação do planeta em torno do Sol.
a. Se a missão falhar, quantas horas levará até que o asteróide atinja a Terra?
b. O raio aproximado da Terra é de 6.400 km. Em que valor mínimo de ângulo o asteróide deve ser desviado a fim de não atingir a Terra?
c. O motor do foguete funciona ao máximo durante 300 s antes que acabe o combustível. A Terra será salva?
Agora tudo faz sentido, não é mesmo? O foguete não é pra explodir o asteroide, é pra empurra ele longe da Terra. Que confusão!
Bora fazer o exercício então.
Passo 2
a)
Aqui precisamos descobrir quanto tempo vai demorar para o asteroide atingir a Terra. E nós temos a velocidade dele e a ditância até a Terra, entãooo
Isolando o tempo
Como a velocidade esta em e a distância esta em não precisamos transformar os dois para metro, pois o quilometro vai cortar com o quilometro. Subistituindo:
Passo 3
b)
Vamos fazer o desenho pra entender melhor que que esta acontecendo:
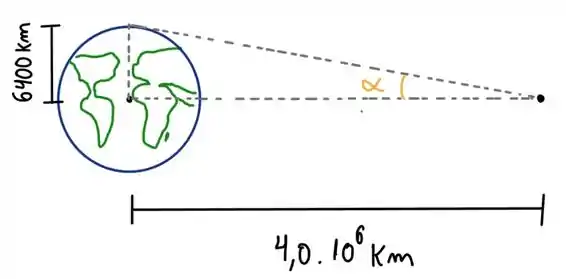
Olha ai, temos um triângulo, para descobrir o ângulo é só calcular a tangente dele:
Calculando esse arcotangente:
Passo 4
c)
Vamos entender esse movimento.
O asteroide vai manter uma velocidade constante em direção a Terra (porque é pra desprezar a gravidade).
O asteroide vai acelerar na direção durante 300 s. Após isso ele vai manter uma velocidade constante em .
Beleza, vamos calcular o quanto o asteroide vai andar na direção de enquanto ele acelera e depois vamos calcular o quanto ele anda na direção de com a velocidade constante. Se essa soma for maior que o raio da Terra, o asteroide não ira colidir.
Primeira parte, com aceleração:
Precismos saber a aceleração do asteroide, pra isso vamos usar a Segunda Lei de Newton:
Vamos calcular quanto ele andou:
Vamos considerar que o .
Como o asteroide estava indo bem retinho em direção a Terra ele não tem velocidade inicial em . A equação fica:
Beleza, agora precisamos descobrir como estava a velocidade desse asteroide quando ele parou de acelerar:
Sabemos que vai demorar para o asteroide chegar a terra, vamos descobrir quanto o asteroide ainda vai se deslocar (Ele já gastou 300 segundos acelerando, temos que descontar isso):
Ou seja, o asteroide vai passar bemm longe da Terra.
Resposta
a)
b)
c)
Sim