Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 9.Problemas - Ex. 13

Um átomo de hidrogênio, movendo com velocidade v, colide com uma molécula de hidrogênio em repouso, sofrendo uma deflexão de 45 ° . Calcule: a) a magnitude da velocidade do átomo após a colisão; b) a direção de movimento da molécula (com respeito à direção inicial de movimento do átomo) e a magnitude de sua velocidade.

Passo 1

  1. Um molécula de hidrogênio são 2 átomos de hidrogênio, resumindo : a partícula alvo tinha 2 vezes a massa do projétil.

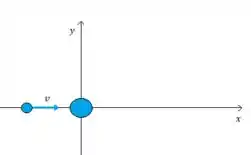
  • Situação inicial

  • Situação final

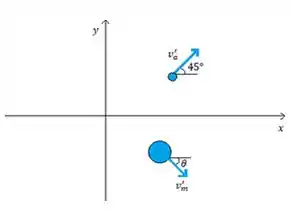
    • Pela conservação do momento, já que só atuam forças internas na colisão temos

    P ⃑ i = P ⃑ f

    Vamos olhar no esquema

  • Aqui P ⃑ a representa P ⃑ i

  • P ⃑ a ' + P ⃑ m ' é o P ⃑ f

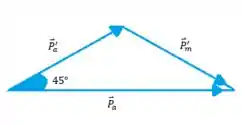
    • Bora usar a lei dos senos para determinar uma relação entre os momentos iniciais e finais do sistema

    P m ' 2 = P a ' 2 + P a 2 - 2 P a ' P a c o s 45 °

    =   P a ' 2 + P a 2 - P a ' P a 2  

    Show, para conseguir as outras informações vamos usar o fato de que a colisão é totalmente elástica, ou seja, a energia cinética se conseva

    T i = T f  

    Escrevendo em função dos momentos das partículas ficamos com

    P a 2 2 m = P a ' 2 2 m + P m ' 2 4 m

    →

    P m ' 2 = 2   P a 2 - P a ' 2

    Ae, galera, é só juntar nossas duas formulinhas e tirar o P m ' 2 , olha só

    P a ' 2 + P a 2 - P a ' P a 2 = 2   P a 2 - P a ' 2

    →

    P a 2 - 3   P a ' 2 + P a ' P a 2 = 0

    Agora é só escrever nossos momentos em função das velocidades. Um deltahe, a velocidade inicial do átomo v a é igual ao v dado no problema!

    m 2 v 2 - 3 m 2 v a ' 2 + m 2 v v a ' 2 = 0

    Dividindo os 2 lados pelas massas,

    - 3 v a ' 2 + v 2 v a ' + v 2 = 0

    Opa, temos uma equação de segundo grau para v a ' !

    a =   - 3

    b = v 2

    c = v 2

    v a ' = - v 2 ± 2 v 2 + 12 v 2 - 6

    = - v 2 ± v 14 - 6

    = - 0,39 v   o u   0,86 v

    Como v a ' está no mesmo sentido que v   então,

    v a ' = 0,86 v

    Passo 2

  • Para descobrir o ângulo θ vamos usar a conservação de momento separando as componentes, olhando pras figuras iniciais temos

  • Conservação do momento na componente x

    • m v = m v a ' c o s 45 ° + 2 m v m ' c o s θ

    v - v a ' c o s 45 ° 2 = v m ' c o s θ

    Já que v a ' = 0,86 v vamos substituir

    v 2 1 - 0,86 2 = v m ' c o s θ

  • Pela conservação do momento em y

0 = m v a ' s e n 45 ° - 2 m v m ' s e n θ

→

v m ' s e n θ = v a ' 2 s e n 45 °

= 0,86 v 2 2

Ae, agora a gente divide a equação de baixo pela de cima e tá no papo.

v m ' s e n θ v m ' c o s θ = 0,86 v 2 2 v 2 1 - 0,86 2

→

t g θ = 0,86 2 1 - 0,86 2

= 0,86 2 - 0,86

= 1,55

θ = a r c t g 1,55

= 57 °

Passo 2

Pra saber a velocidade final da molécula v m ' vamos pegar uma das equações acima

v m ' s e n θ = 0,86 v 2 2

Isolando v m '

v m ' = 0,86 v 2 2 s e n 57 °

= 0,36 v

Resposta

a )   0,86 v

b )   57 °   e   0,36 v

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 9-59, uma bala de 10g que se move verticalmente para cima a 1000m / s se choca com um bloco de 5,0k g inicialmente em repouso, passa pelo centro de massa do bloco e sai do outro lado com uma v
Na Fig. 9-63, o bloco 1 (com uma massa de 2,0k g ) está se movendo para a direita com uma velocidade escalar de 10m / s e o bloco 2 (com uma massa de 5,0k g ) está se movendo para a direita com uma ve
Uma bala com 10g de massa se choca com um pêndulo balístico com 2,00k g de massa. O centro de massa do pêndulo sobe uma distância vertical de 12c m . Supondo que a bala fica alojada no pêndulo, calcul
Na Fig. 9-61, uma bola de massa m=60g é disparada com velocidade v i =22m / s para dentro do cano de um canhão de mola de massa M=240g inicialmente em repouso sobre uma superfície sem atrito. A bola f
Em Anchorage, as colisões de um veículo com um alce são tão comuns que receberam o apelido de CVA. Suponha que um carro de 1000k g derrapa até atropelar um alce estacionário de 500k g em uma estrada m