Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 22

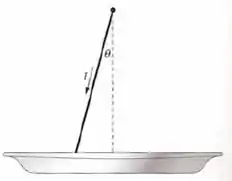
Em sua aula de laboratório de física, você construiu um gaussímetro simples para medir a componente horizontal de campos magnéticos. A montagem consiste em um fio firme de 50   c m que está suspenso verticalmente em um pivô condutor e sua extremidade livre faz contato com um recipiente contendo mercúrio (figura abaixo). O mercúrio fornece um contato elétrico sem restringir o movimento do fio. O fio tem massa de 5,0   g e conduz corrente para baixo. (a) Qual é o deslocamento angular de equilíbrio do fio a partir da vertical se a componente horizontal do campo magnético é 0 , 040   T e se a corrente é 0,20   A ? (b) Qual é a sensibilidade deste gaussímetro? Isto é, qual é a razão da saída para a entrada (em radianos por tesla)?

Passo 1

OI OI OI, estamos aqui para mais uma questão, envolvendo força magnética. Para entendermos melhor a questão, observe o diagrama abaixo:

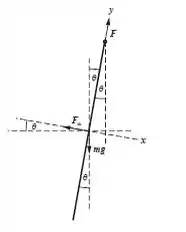
O campo magnético aponta para fora da página (direto nos seus olhos, baby). O diagrama nos mostra que o gaussímetro é retirado do equilíbrio sobre a influência da força gravitacional, magnética e a que é exercida pelo pivô condutor. DITO ISTO, podemos utilizar as condições de equilíbrio de translação na direção x para encontrar o equilíbrio do deslocamento angular do fio na vertical! Para calcular a sensitividade do gaussímetro basta resolver a equação obtida na letra (a) e fazermos uma razão por B . (AGORA VAMOS COLOACAR AS MÃOS NA MASSA).

Passo 2

Primeiramente, vamos aplicar o equilíbrio no eixo x:

W x =   F m

m   g   s i n θ =   F m

-   F m + m   g   s i n θ =   0 (1)

Na magnitude F m a g = I   l   B   s i n ∅ , o ângulo ∅ = 90 ° , então:

F m a g = I   l   B

Substituindo na equação 1, temos que:

-   I   l   B + m   g   s i n θ =   0

m   g   s i n θ = I   l   B

s i n θ = I   l   B m   g    

θ = sin - 1 ⁡ I   l   B m   g  

Substituindo as variáveis pelos valores dados na questão obteremos o ângulo de deslocamento do equilíbrio:

θ = sin - 1 ⁡ 0.20   A 0.50 m ( 0.040   T ) ( 0.0050 k g )   ( 9.81   m / s 2 )

θ = 4.679 °

θ = 4.7 °

θ = 82 m r a d

LETRA (A) feita! agora, vamos para a letra (b).

Passo 3

Podemos definir a sensibilidade pela razão da saída e da entrada, ou seja:

s e n s i b i l i d a d e = θ B

s e n s i b i l i d a d e = 82 m r a d 0.040   T

s e n s i b i l i d a d e = 2.0   r a d / T

AÍ ESTÁ, tudo feito com sucesso!

É TUDO POR HOJE, bons estudos ;)

Obs: Vai beber água que ta na hora, obrigado, de nada.

Resposta

(a)   θ = 82 m r a d

(b)   s e n s i b i l i d a d e = 2.0   r a d / T

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Certo cíclotron, cujo campo magnético tem intensidade igual a 1,8T , é projetado para acelerar os prótons até a energia cinética de 25M e V . (a) Qual é a frequência de cíclotron para esse dispositivo
Um feixe de íons de L i 6 e L i 7 monovalentes passa por um seletor de velocidades e entra em uma região de campo magnético uniforme, com velocidade perpendicular à direção de campo. Se o diâmetro da
O campo magnético galáctico em alguma região do espaço interestelar tem magnitude de 1,00x10 - 9T . Uma partícula de poeira interestelar tem massa de 10,00μ g e carga total de 0 , 300n C . Quantos ano
Um próton com rapidez igual a 1,00x10 6m / s entra em uma região com um campo magnético uniforme com magnitude igual a 0,800 T, que aponta para dentro da página, como mostrado na figura abaixo. O prót
Um feixe de prótons está se movendo na direção +x com rapidez de 12,4k m / s através de uma região na qual o campo elétrico é perpendicular ao campo magnético. O feixe não sofre deflexão nesta região.