Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 25
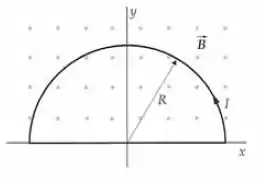
Um fio conduzindo corrente é curvado em um semicírculo fechado de raio que está no plano (Figura 26-34). O fio está em um campo magnético uniforme que está na direção , como mostrado. Verifique que a força exercida no anel é zero.
Passo 1
Olá pessoal, tudo certo com vocês? Espero que sim 😊. Vamos entender melhor essa questão?
Observe que, com a corrente na direção indicada e o campo magnético na direção , apontando para fora do plano da página, a força está na direção radial e podemos integrar o elemento de força atuando sobre um elemento de comprimento entre e para encontrar a força atuando sobre a porção semicircular do laço e usar a expressão para a força sobre um fio portador de corrente em um campo magnético uniforme para encontrar a força sobre o segmento reto do laço.
Passo 2
Ainda sem entender? Vamos para os cálculos que vai facilitar a visualização. Observe a imagem abaixo:
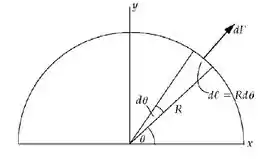
Certo! Vamos expressar a força líquida atuando sobre o laço semicircular do fio:
Agora expressando a força atuando no laço do segmento reto, temos:
Certo! Temos que expressar a força atuando no fio de comprimento :
Expressando agora as componentes e de
Passo 3
Observe que, por causa da simetria, a força na componente é zero, assim nós podemos integrar a componente para achar a força no fio, desse modo:
Resolvendo, temos
Passo 4
Logo,