Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 38
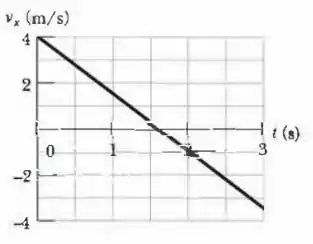
Uma caixa com uma massa de sobe uma rampa sem atrito que faz um ângulo com a horizontal. A Fig. 5-41 mostra, em função do tempo , a componente , da velocidade da caixa ao longo de um eixo orientado para cima ao longo da rampa. Qual é o módulo da força normal que a rampa exerce sobre a caixa?
Passo 1
Nessa questão, precisamos ter em mente a segunda lei de Newton:
Que pode ser expandida para a definição das componentes escalares:
Além disso, precisamos lembrar a função da velocidade do MRUV:
Porém, nesta questão, não foi dado os dados diretamente e sim um gráfico onde podemos extrair os pontos para determinar esta função. A partir desta função, conseguimos determinar qual a aceleração para substituir na segunda lei de Newton. Parace que vai dar um trabalhão, né? Mas, relaxa, vamos separar a questão em pequenos pedaços para fluir melhor, show?!
Este problema nos dá a massa da caixa (), o gráfico da velocidade em função do tempo e nos pede para determinar a força normal.
Passo 2
Inicialmente vamos determinar a função velocidade extraindo dois pontos do gráfico:
Vamos substituir esses dois pontos na função da velocidade:
Agora, substituindo o segundo ponto:
Assim, temos que:
E, por isso, temos que a aceleração é:
Passo 3
Agora, vamso escrever a segunda lei de Newton para as componentes. Para isso, vamos fazer o DCL para facilitar nossa visualização:
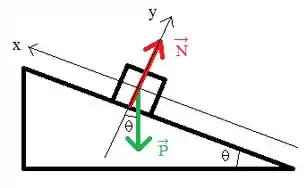
Então, escrevendo a segunda lei de Newton para a componente :
Substituindo os valores:
Isolando :
Isolando :
Passo 4
Escrevendo a segunda lei de Newton para a componente :
Sabendo que não há movimento no eixo e substituindo os valores:
Isolando o :