Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 40
Um esquiador de é puxado para o alto de uma encosta sem atrito segurando um cabo que se move paralelamente à encosta, que faz um ângulo de com a horizontal. Qual é o módulo da força que o cabo exerce sobre o esquiador (a) se o módulo da velocidade do esquiador é constante e igual a e (b) se aumenta a uma taxa de ?
Passo 1
Show de bolinhas pessoal, pra gente iniciar essa questão precisamos ter em mente que a força resultante que age sobre um corpo é a soma de todas as forças que atuam no mesmo e está relacionada à aceleração pela definição da segunda lei de Newton:
Lembrando que podemos aplicar a segunda lei de Newton para cada componente:
Aqui precisamos sacar que a lei de Newton tem relação com a aceleração e não, diretamente, com a velocidade. Então, quando a velocidade for constante, a aceleração será nula e concomitantemente a força resultante também será nula. Então quando o enunciado fala sobre taxa de variação da velocidade, ele está falando da aceleração.
Este problema nos dá a massa do esquiador (), o ângulo que a encosta faz com a horizontal (), fala que a encosta não tem atrito e pede para determinarmos o módulo da força que o cabo exerce sobre o esquiador para duas situações ( e ).
Passo 2
Para iniciar, vamos fazer um diagrama do corpo livre para entender melhor como as forças estão atuando, beleza?
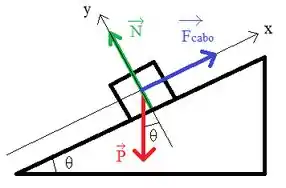
A partir dessa ilustração, podemos escrever as leis de Newton para cada eixo, porém como nesta questão a força que desejamos determinar está no eixo , vamos focar nesse eixo. Assim:
Substituindo os valores conhecidos, obtemos que:
Passo 3
Para o caso da velocidade ser constante, temos que , portanto, substituindo essa informação na , temos:
Isolando :
Passo 4
Para o caso que a aceleração é , fazemos de maneira análoga ao passo anterior, tal que:
Isolando :
Resposta
- ;
- .