Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 19
Na Fig. 5-36, a massa do bloco é e o ângulo é .Determine (a) a tensão na corda e (b) a força normal que age sobre o bloco. (c) Determine o módulo da aceleração do bloco se a corda for cortada.
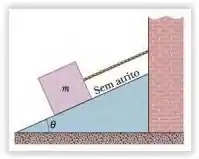
Passo 1
Então galera , bora dar uma olhada no esquema que mostra o diagrama de corpo livre da situação . Como a aceleração do bloco é zero, a Segunda Lei de Newton nos dá :
na qual é a tração da corda e é a força normal que age sobre o bloco.
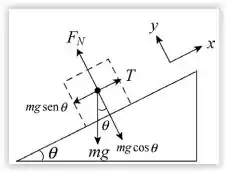
Isolando na primeira equação, temos que :
Passo 2
Agora podemos isolar na equação através da relação :
Passo 3
Agora temos que perceber que quando a corda é cortada, deixa de exercer uma força sobre o bloco e o bloco começa a acelerar. Aplicando a Segunda Lei de Newton à componente do peso, temos que :
O que nos dá :
O sinal negativo indica que a aceleração é para baixo. O módulo da aceleração é
De boa pessoal ??? Bora resolver mais questões então!!!!!
Resposta
Ei, a resposta está no passo a passo :)