Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 56

No arremesso de peso, muitos atletas preferem lançar o peso com um ângulo menor que o ângulo teórico (cerca de 42 ° ) para o qual a distância é máxima para um peso arremessado com a mesma velocidade e da mesma altura. Uma razão tem a ver com a velocidade que o atleta pode imprimir ao peso durante a fase de aceleração. Suponha que um peso de 7,260   k g é acelerado ao longo de uma trajetória reta com 1,650   m de comprimento por uma força constante de módulo 380,0   N , começando com uma velocidade de 2,500   m / s (devido ao movimento preparatório do atleta). Qual é a velocidade do peso no final da fase de aceleração se o ângulo entre a trajetória e a horizontal é (a) 30,00 ° e (b) 42,00   ° ? (Sugestão: trate o movimento como se fosse ao longo de uma rampa com o ângulo dado.) (c) Qual é a redução percentual da velocidade de lançamento se o atleta aumenta o ângulo de 30,00 ° para 42,00 ° ?

Passo 1

Beleza galerinha, esse é um problema que assusta um pouco pelo texto grande, mas vamos tentar extrair dele somente a parte necessária.

Primeiro, há uma parte da trajetória que tem uma força constate de módulo 380   N , cuja a distância dessa etapa é de 1,65   m . Nós sabemos que o peso já inicia essa trajetória com uma velocidade inicial de 2,5   m/s e o próprio enunciado nos dá a sugestão de considerarmos este movimento como se fosse ao longo de uma rampa com os ângulos dados. Assim, para facilitar nossa visualização, vamos fazer um diagrama de corpo livre, tal que:

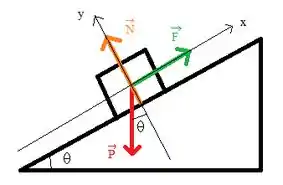
Vamos escrever a segunda lei de Newton para a componente x para podermos determinar a aceleração e então usando a equação de Torricelli conseguir determinar a velocidade final:

F - P sin ⁡ θ = m a

Passo 2

Agora vamos substituir os valores do primeiro caso na equação acima:

380 - 7,26 × 9,8 × sin ⁡ 30 ° = 7,26   a

Isolando o a :

a = 47,44   m/ s 2

Com a aceleração em mãos, podemos substituir na equação de Torricelli para determinar a velocidade final:

v f 2 = v 0 2 + 2 a ∆ x

v f 2 = 2,5 2 + 2 × 47,44 × 1,65

Isolando v f :

v f = 2,5 2 + 2 × 47,44 × 1,65

v f = 12,76   m/s

Passo 3

Para o caso dois, faremos de maneira análoga, mudando apenas o valor do ângulo:

380 - 7,26 × 9,8 × sin ⁡ 42 ° = 7,26 a

Isolando o a :

a = 45,78   m/s²

Aplicando Torricelli:

v f 2 2 = v 0 2 + 2 a 2 ∆ x

v f 2 2 = 2,5 2 + 2 × 45,78 × 1,65

Isolando v f 2 :

v f 2 = 2,5 2 + 2 × 45,78 × 1,65

v f 2 = 12,54   m/s

Passo 4

Para calcularmos a redução percentual:

R % = v f - v f 2 v f × 100

R % = 1,7 %

Resposta

  1. v f = 12,76   m / s ;
  2. v f 2 = 12,54   m / s ;
  3. R = 1,7 % .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro acelera descendo uma colina (Fig. P4.57), partindo do repouso a 30,0m / s em 6,00s . Um brinquedo dentro do carro está pendurado por um fio no teto. A bola na figura representa o brinquedo de
Um bloco de massa m=2,00k g é liberado do repouso a h=0,500m acima da superfície de uma mesa, no topo de um plano inclinado com θ=30,0 ° , conforme mostrado na Figura P4.53. O plano inclinado é fixado
Um plano sem atrito tem 10,0m de comprimento e 35,0 ° de inclinação. Um trenó começa na parte de baixo com velocidade inicial de 5,00m / s subindo o declive. Quando ele alcança o ponto no qual momenta
Uma cunha de massa M repousa sobre o topo horizontal de uma mesa sem atrito. Um bloco de massa m é colocado sobre a cunha (Figura P5.112a). Não existe nenhum atrito entre o bloco e cunha. O sistema é
Uma cunha de massa M repousa sobre o topo horizontal de uma mesa sem atrito. Um bloco de massa m é colocado sobre a cunha e uma força horizontal F é aplicada sobre ela (Figura P5.112b). Qual deve ser