Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 111
O avião A está voando para o leste com uma rapidez em relação ao ar de 400 mph. Diretamente abaixo, a uma distância de 4000 ft, o avião B está apontado para o norte, voando com uma rapidez em relação ao ar de 700 mph. Encontre o vetor velocidade do avião B em relação ao avião A.
Passo 1
E aí pessoal, beleza? O assunto pra essa questão é movimento relativo. Nesse tipo de questão devemos ter bastante atenção e organização para não misturar os vetores. A figura abaixo vai nos ajudar a entender melhor o problema.
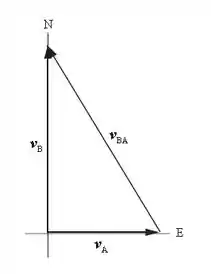
Temos representando o vetor velocidade do avião A e , representando o vetor velocidade do avião B. A velocidade de B em relação a A é exatamente o vetor .
Passo 2
Agora que já sabemos a relação temos que usar a notação vetorial para escrever as expressões da velocidade.
O avião A está indo para leste. Em um plano cartesiano essa direção representa o eixo positivo.
Já o avião B está indo para norte. Em um plano cartesiano repreenta o eixo y posivito.
Podemos obter :
Passo 3
Agora que já temos os valores na forma vetorial, vamos substituir na equação para encontrarmos o valor da consulta.