Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 67
A Terra gira em torno de seu eixo uma vez a cada 24 horas, de forma que os objetos em sua superfície executam movimento circular uniforme em torno do eixo com um período de 24 horas. Considere apenas o efeito desta rotaçãosobre uma pessoa na superfície. (ignore o movimento orbital da terra em torno do Sol.) (a) Qual é a rapidez, e qual é a magnitude da aceleração de uma pessoa no equador? (Expresse a magnitude desta aceleração como uma porcentagem de g.) (b) Qual é a orientação do vetor aceleração? (c) Qual é a rapidez e qual é a magnitude da aceleração de uma pessoa na superfície, a 35° de latitude norte? (d) Qual é o ângulo entre o sentido da aceleração da pessoa a 35° de latitude norte e o sentido da aceleração da pessoa no equador, se as duas pessoas estão em uma mesma longitude?
Passo 1
a) Oi pessoal, tudo bem? Vamos analisar essa questão. Ele diz que a Terra gira em torno de um eixo e sempre leva para dar uma volta completa, ou seja, temos rapidez constante. E pede a aceleração e rapidez de uma pessoa no equador.
Essa pessoa na superfície da Terra está em uma trajetória circular já que a Terra gira e ela está sobre a Terra. Assim, a aceleração que essa pessoa vai ter vai ser a aceleração centrípeta. Mas o que ele quer dizer com ela está na linha do equador?
Vamos lembrar um pouco de Geografia da escola, a linha do equador é a linha imaginária em torno do meio do planeta:
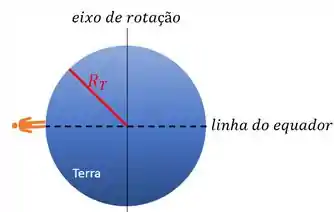
Isso quer dizer que a trajetória da pessoa em torno do eixo de rotação da Terra tem raio igual ao raio da Terra
Com isso em mente e sabendo que a gente tem um movimento circular de rapidez constante, vamos calcular o que ele pede!
Passo 2
Por definição, a aceleração centrípeta é dada por:
Sendo que é o raio da trajetória e é o módulo da velocidade do movimento circular.
O módulo da velocidade (a rapidez) para o movimento circular é dado por:
Onde , é o período de rotação que é o tempo de a Terra dá uma volta completa. Vimos que esse tempo é de , mas precisamos passar esse cara para segundos
Vimos que , e pelo apêndice B, temos . Temos então que a velocidade é de:
Com isso, a aceleração centrípeta será:
Mas ele quer esse resultado como uma porcentagem de . Então vamos fazer uma regrinha de 3:
Passo 3
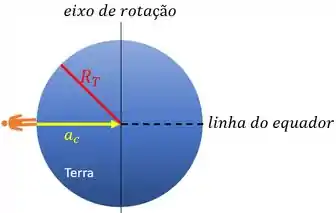
b) Por definição o vetor aceleração centrípeta aponta para o centro da trajetória, logo, o vetor aceleração aponta diretamente para o centro da Terra.
Passo 4
c) Ele quer as mesmas grandezas, mas agora a pessoa está a de latitude norte. Ou seja, ela está numa linha imaginária mais acima da linha do equador:
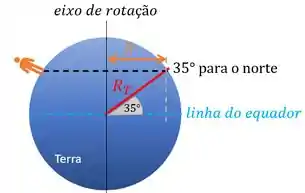
Isso quer dizer que o raio da sua trajetória em relação ao eixo de rotação não é mas menor. Para achar esse raio podemos usar trigonometria. Percebe que o raio da nossa trajetória tem o mesmo tamanho que a projeção de na horizontal.
Para achar o valor de , podemos fazer:
Agora a gente pode usar as fórmulinhas da rapidez e da velocidade. Temos:
Subsituindo:
A aceleração centrípeta será:
Passo 5
d) Cara, ele quer o ângulo entre o vetor aceleração para o primeiro caso e o vetor aceleração para esse caso que a gente acabou de avaliar.
Para isso, vamos posicionar o vetor aceleração para esse segundo caso. O vetor aponta sempr para o centro da trajetória. Como agora nossa trajetória é uma circunferência mais acima, nosso vetor vai apontar para o centro dela e não o centro da Terra. Fica assim:
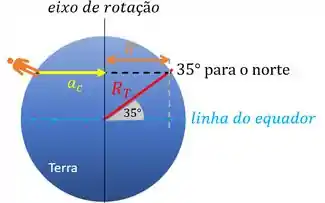
Aí vamos avaliar as duas situações juntas:
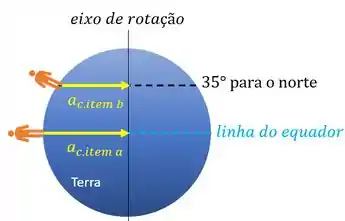
Percebe que as acelerações são ambas perpendiculares ao eixo de rotação. Isso faz com que elas sejam paralelas entre si.
Logo o ângulo entre elas é nulo.
Resposta
Por definição o vetor aceleração centrípeta aponta para o centro, logo, o vetor aceleração aponta diretamente para o centro da Terra.