Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 8.Problemas - Ex. 57

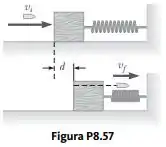
Uma bala de 5,00   g   movendo-se com velocidade inicial de v   =   400   m / s é atirada contra um bloco de 1,00   k g e passa através dele, como mostrado na Figura P8.57. O bloco, inicialmente em repouso em uma superfície horizontal sem atrito, é conectado a uma mola com constante de força 900   N / m . O bloco move-se por uma distância d   =   5,00   cm para a direita, depois do impacto, antes de ser trazido ao repouso pela mola. Encontre (a) a velocidade com a qual a bala emerge do bloco e (b) a quantidade de energia cinética inicial da bala que é convertida em energia interna no sistema bala-bloco durante a colisão.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

Encontre a velocidade quando a bala surge do bloco usando a conservação o momento:

m v i = M V i + m v

O bloco se move a uma distância de 5.00cm. Suponha que seja uma aproximação de que o bloco atinge rapidamente a velocidade máxima, V, e a bala continua com uma velocidade constante, v. O bloco então comprime a mola e para.

Após a colisão, a energia mecânica é conservada no sistema:

1 2 M V i 2 = 1 2 k x 2 V i = 900 N m 5.00 × 10 - 2 m 2 1.00 k g = 1.50 m / s v = m v i - M V i m = 5.00 × 10 - 3 k g 400 m s - 1.00 k g 1.50 m s 5.00 × 10 - 3 k g v = 100 m / s

Passo 2

Letra b:

Antes da colisão:

Δ K + Δ E int  = 0   n o s   d á :   Δ E int  = - Δ K = - 1 2 m v 2 + 1 2 M V i 2 - 1 2 m v i 2

Então,

Δ E int  = - 1 2 ( 0.00500 k g ) ( 100 m / s ) 2 + 1 2 ( 1.00 k g ) ( 1.50 m / s ) 2 - 1 2 ( 0.00500 k g ) ( 400 m / s ) 2

= 374 J

Resposta

  1. 100 m / s
  2. 374 J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula A e uma partícula B são empurradas uma contra a outra, comprimindo uma mola colocada entre as duas. Quando as partículas são liberadas, a mola as arremessa em sentidos opostos. A massa d
Na Fig. 9-57, um bloco inicialmente em repouso explode em dois pedaços, E eD , que deslizam sobre um piso em um trecho sem atrito e depois entram em regiões com atrito, onde acabam parando. O pedaçoE
Três discos de hóquei idênticos possuindo imãs que se repelem estão sobre uma mesa de ar horizontal. Eles são mantidos unidos e a seguir são libertados simultaneamente. O módulo da velocidade em cada
Um núcleo de ²¹⁰Bi (bismuto) em repouso sofre decaimento beta para o núcleo de beta para núcleo de ²¹⁰Po (polônio). Suponha que o elétron emitido se move da esquerda para a direita com um momento line
Daniel (massa de 65,0 kg) e Rebeca (massa de 45,0 kg)estão praticando patinação sobre uma pista de gelo. Enquantoestá parado amarrando o cordão de seu patim, Daniel é atingidopor Rebeca, que se desloc