Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 10º - Capítulo 8.Exercícios - Ex. 22

Daniel (massa de 65,0 kg) e Rebeca (massa de 45,0 kg)

estão praticando patinação sobre uma pista de gelo. Enquanto

está parado amarrando o cordão de seu patim, Daniel é atingido

por Rebeca, que se deslocava a 13,0 m/s antes de colidir com ele.

Depois da colisão, a velocidade de Rebeca possui módulo igual

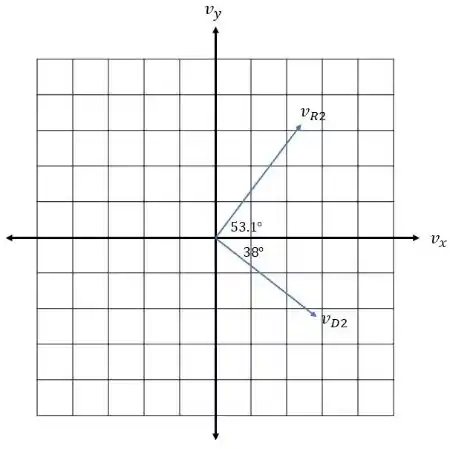
a 8,0 m/s e forma um ângulo de 53,1º com a direção de sua ve-

locidade inicial. Ambos se movem sobre a superfície horizontal

sem atrito da pista de gelo. (a) Quais são o módulo, a direção e

o sentido da velocidade de Daniel depois da colisão? (b) Qual é

a variação da energia cinética total dos dois patinadores como

resultado da colisão?

Passo 1

Beleza pessoal?! Espero que esteja tudo bem com meu os herdeiros de Newton. Vamos dar início a mais uma resolução com o padrão de qualidade do Responde aí, então pegue seu lápis, caderno e café e vamos nessa!!!

Temos que a massa de Daniel é mD=65,0 e a massa de Rebecca é mR=45,0. Seja +x na direção inicial de Rebeca e +y na direção que fazem um ângulo 36,9 ° com a velocidade final dela, então temos:

v R 1 x = 13.0   m / s /   v R ! x = 0

V R 2 x = 8.00   c o s   53.1   =   4.80   m / s ,   v R 2 y = 8.00   s i n   53.1   =   6.40   m / s

V D 1 x = 0 ,   v D 1 y = 0

V D 1 x = ? ? ? ,   v D 1 y = ? ? ?

Passo 2

Sabemos que o momento total de um sistema é a soma vetorial dos momentos das partículas individuais que compõem o sistema:

p _ = p _ A + p _ B + .   .   .

Se o movimento estiver em um plano (duas dimensões), a equação se torna:

p x = p x A + p x B +   .   .   .

p y = p y A + p y B + .   .   .

Onde os momentos de uma partícula são dados por:

p _ = m v _

Sabemos também, para um sistema isolado, cada componente do momento do sistema é conservado separadamente, então:

Como a superfície não tem atrito, o sistema (Daniel e Rebecca) é isolado (neste plano).

Aplicando a conservação do momento, o momento do sistema antes da colisão é igual ao momento do sistema após a colisão, então obtemos:

p 1 x = p 2 x

p 1 y = p 2 y

Aplicando as equações (1) e (3), obtemos:

p D 1 x + p R 1 x = p D 2 x + p R 2 x

p D 1 y + p R 1 y = p D 2 y + p R 2 y

Agora, aplicando a equação (2) a Daniel e Rebecca e substituindo na equação (4), obtemos:

m D v D 1 x + m R v R 1 x = m D v D 2 x + m R v R 2 x

m D v D 1 + m R v R 1 y = m D v D 2 y + m R v R 2 y

Agora, colocamos nossos valores para mD, mR, vD1xv, vR1x e vR2x na equação (5), então obtemos:

( 65.0 ) ( 0 ) + ( 45 ) ( 13.0 ) = ( 65.0 ) v D 2 x + ( 45.0 ) ( 4.80 )

v D 2 x = 5.67   m / s

E inserimos nossos valores para mDm, mR, vD1y​, vR1y​ e vR2y na equação (6), então obtemos:

( 65.0 ) ( 0 ) + ( 45 ) ( 0 ) = ( 65.0 ) v D 2 y + ( 45.0 ) ( 6.40 )

v D 2 x = - 4.43   m / s

Assim, o módulo da velocidade de Daniel após a colisão é:

v D 2 = v ² D 2 x + v ² D 2 y = 7.20   m / s

θ = t a n   ⁻ ¹ v D 2 y v D 2 x = t a n ⁻ ¹ - 4.43 5.67 = - 38.0 ⁰

Resposta

Ver o desenvolvimento

Exercícios de Livros Relacionados

Uma partícula A e uma partícula B são empurradas uma contra a outra, comprimindo uma mola colocada entre as duas. Quando as partículas são liberadas, a mola as arremessa em sentidos opostos. A massa d
Os gases que se expandem ao deixar o cano de um rifletambém contribuem para o recuo. Uma bala de calibre 30 possuimassa igual a 0,00720 kg e velocidade de 601 m/s em relação aocano, quando disparada d
Três discos de hóquei idênticos possuindo imãs que se repelem estão sobre uma mesa de ar horizontal. Eles são mantidos unidos e a seguir são libertados simultaneamente. O módulo da velocidade em cada
Um núcleo de ²¹⁰Bi (bismuto) em repouso sofre decaimento beta para o núcleo de beta para núcleo de ²¹⁰Po (polônio). Suponha que o elétron emitido se move da esquerda para a direita com um momento line