Na Fig. 9-57, um bloco inicialmente em repouso explode em dois pedaços, e, que deslizam sobre um piso em um trecho sem atrito e depois entram em regiões com atrito, onde acabam parando. O pedaço, com uma massa de , encontra um coeficiente de atrito cinético e chega ao repouso em uma distância . O pedaço encontra um coeficiente de atrito cinético e desliza até o repouso em uma distância . Qual era a massa do bloco?
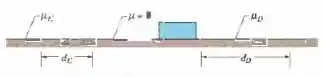
Passo 1
Oi, galerinha! Tudo bom? A boa desse exercício é pensar no bloco deslizando até parar, onde a energia cinética será convertida em energia térmica, através do atrito. Onde não tem atrito não tem perda de energia cinética. Isso significa que o trabalho do atrito será igual à energia cinética com que ele entra na região.
Como estamos falando de atrito cinético, então o atrito será
Onde usamos que o módulo da normal é igual ao módulo do peso. Assim
Isolando
Separadamente, para cada um dos dois pedaços, temos que :
Assim, podemos dividir essas duas expressões
Passo 2
Bom pessoal , sabemos que por outro lado, de acordo com a lei de conservação do momento, como o momento do bloco completo antes da explosão era nulo, temos que
Onde estabelecemos que velocidade para esquerda é negativa e para direita é positiva.
Assim
Já calulamos essa razão no passo anterior. Assim substituindo
Dessa forma , a massa total é .
Resposta
Traquilo galera? Bora resolver mais questões então!