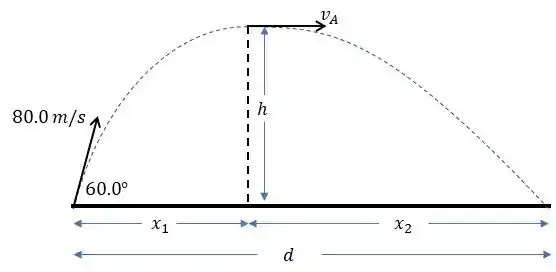
Um projétil de 20.0 kg é disparado com velocidade de

80,0 m/ s formando um ângulo de 60,0⁰ acima da horizontal. No ponto mais elevado de sua trajetória o projétil explode se dividindo

em dois fragmentos de mesma massa , um dos quais cai

verticalmente com velocidade inicial igual a zero. Despreze a

resistência , a ) Supondo um solo horizontal , qual é a distância entre

o ponto inicial do disparo e o pomo onde o segundo fragmento atinge

o solo? b ) Qual é a quantidade de energia libertada na explosão?

Temos três estágios, o primeiro estágio é o movimento do projétil até seu ponto mais alto, o segundo estágio é a explosão e o terceiro estágio é o movimento do fragmento do ponto de explosão ao ponto de pouso.

O primeiro estágio:

Sabemos, do capítulo 3, que no movimento de projéteis podemos tratar separadamente o movimento horizontal e o vertical.

Primeiro, tomamos +x na direção horizontal e +y para cima.

Para a direção vertical: o projétil se move com uma aceleração constante negativa igual a −g ​​e a velocidade vertical inicial é a componente vertical da velocidade inicial, então temos:

Este é o tempo que o projétil leva para atingir seu ponto mais alto.

Agora, colocamos nossos valores para t1​ em uma equação cinemática adequada para obter o ponto mais alto hh da seguinte forma:

Para o movimento horizontal: o projétil se move com uma velocidade constante que é igual à componente horizontal da velocidade inicial, então temos:

Agora, usamos o valor de t1​ para obter a distância horizontal entre o ponto de disparo até o ponto mais alto da seguinte forma:

Como mencionamos no primeiro estágio, a velocidade vertical no ponto mais alto é zero zero; Assim, a velocidade do projétil imediatamente antes da explosão é:

Substituindo na equação (1), temos:

Como não há força resultante externa do projétil durante a explosão, o momento do sistema é conservado.

Assim, o momento do projétil antes da explosão é igual ao momento total dos dois fragmentos após a explosão:

Mas um dos fragmentos (digamos B) começa a cair com velocidade inicial zero após a explosão, então obtemos:

Substituindo na equação (1), sabendo que a massa do fragmento é metade da massa do projétil mA​=m/2, obtemos:

Assim, após a explosão, o outro fragmento A passa a se mover como um novo projétil com velocidade inicial vA​=80,0 na direção horizontal.

Para o movimento vertical, substituímos yi​=h, yf​=0, ya​=−9.8 m/s e vAiy​=0 em uma equação cinemática adequada, então obtemos :

Este é o tempo que leva para o fragmento atingir a terra.

Agora, obtemos a distância horizontal entre o ponto de explosão ao ponto de terra da seguinte forma:

Assim, a distância horizontal entre o ponto de disparo e o ponto onde o outro fragmento de terra é:

A energia liberada da explosão é a variação da energia cinética total do sistema, então temos: