Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 64
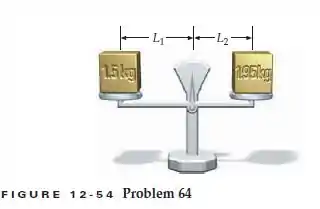
Uma balança tem braços desiguais. Ela é equilibrada com um bloco de 1,50 kg no prato da esquerda e um bloco de 1,95 kg no bloco da direita (Figura 12-54). Se o bloco de 1,95 kg é removido do prato da direita e bloco de 1,50 kg é levado ao bloco da direita, qual é a massa que, colocando no prato da esquerda, equilibrará a balança?
Passo 1
Fala! Então, vamos entender o que está acontecendo com essa balança diferentona. A balança suporta o peso dos dois blocos. Podemos entender que os dois braços da balança formam juntos um corpo extenso.
Falou de corpo extenso, a gente já pensa logo em fazer o diagrama de corpo livre! E como ele fica? Bem, para a primeira situação, onde temos as duas massas conhecidas, teremos que essas massas vão transmitir seus pesos ao braço da balança.
Mas por que esse braço não cai? Porque temos uma força de reação , que depende das massas que temos, ali na pecinha que junta o braço da balança à base da balança. Fazendo um diagrama disso, temos
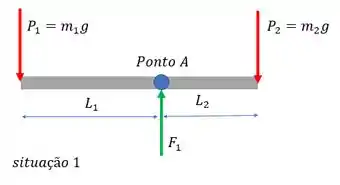
Onde e . Para a segunda situação, ainda temos a mesma coisa. O que muda, é que fica na direita, e na esquerda temos uma nossa massa . E porque as massas mudam, a reação no ponto também muda de valor:
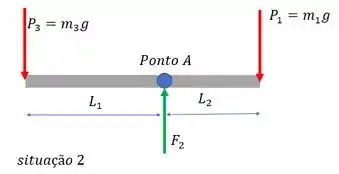
E como esse braço está paradinho, podemos usar as equações de equilíbrio
A ideia é a gente usar essas equações na situação 1 e 2, para resolver nosso problema. E o que ele quer? Ele quer o valor de para termos equilíbrio na situação 2 também. Vamos!
Passo 2
Cara, quem são nossas incógnitas na situação 1? , e , né? A partir disso, podemos começar usando o somatório de torques no ponto para a situação . Por que?
Não conhecemos a reação em , a , e nem queremos conhecer, isso porque ela não aparece na situação 2, já que as massas mudam. Como a gente quer analisar a situação 2 depois, não vai ter muita utilidade.
Aí a gente tem que está aplicada no ponto , por isso ela não gera momento em relação a esse ponto. Então ela não aparece no somatório de torques em .
Assim a gente acha uma relação entre nossas incógnitas e (que vão aparecer na situação 2), sem se preocupar com . Vamos usar então
Onde os torques são calculados por
Onde r é a distância entre a linha de ação da força e o eixo de rotação. e precisam ser perpendiculares. As distâncias estão descritas na figura. Para , a distância entre sua linha de ação e é , e para , temos .
Por convenção, se uma determinada força for capaz de girar o corpo no sentido anti-horário seu sinal será positivo. A força peso do bloco 1 é capaz de girar a barra no sentido anti-horário (+), já a força peso do bloco 2 gira no sentido horário (-). Então nossos torques ficam
Passo 3
Substituindo isso no somatório de torques em relação a :
Lembrando que :
Substituindo e
Achamos a relação existente entre os braços, agora vamos para a segunda condição.
Passo 4
Removemos o bloco de 1,95 kg do prato da direita e substituímos pelo de 1,50 kg, e um terceiro bloco de massa é colocado na esquerda para que se atinja o equilíbrio novamente. Vamos lembrar do diagrama
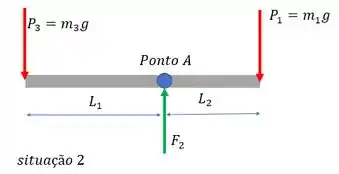
Vamos usar o somatório de torques em de novo, já que só nos interessa e não queremos .
A força peso gera torque no sentido anti-horário com e a força agora gera torque no sentido horário, com . Temos então
Substituindo no somatório
Ficamos então com:
Sabemos que (do passo anterior) e