Júlia foi contratada para ajudar a pintar a fachada de um prédio, mas não está convencida da segurança do equipamento. Uma prancha de é suspensa horizontalmente, do topo do prédio, por cordas presas a cada extremidade. Júlia sabe, da experiência anterior, que as cordas utilizadas se romperão se a tração exceder a . Seu chefe, de , desconsidera as preocupações de Júlia e começa a pintar, quando está a de uma extremidade da prancha. Se a massa de Júlia é e a massa da prancha é , qual é a região que Júlia pode ocupar sobre a prancha, para ajudar o seu chefe, sem provocar o rompimento das cordas?
Passo 1
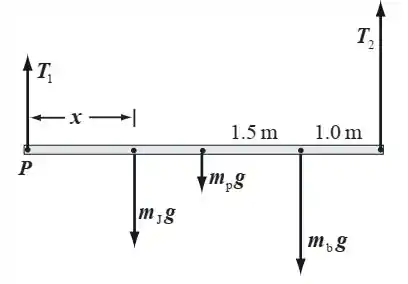
A situação é mais ou menos assim:
Passo 2
Vamos pensar nas condições limite, ou seja, no lugar mais perto e no mais longe que ela pode estar. Tá vendo que, como o chefe dela tá lá na direita, a força já é maior que a força . Então, com a menina em cima da barra, a corda da direita seria a primeira a arrebentar. Então ela vai ser a nossa condição limite! Vamos calcular o momento com relação ao ponto P. faz momento anti-horário e as outras no sentido horário.
Vamos logo extrapolar e jogar a maior tração possível, que é . Isso vai dar:
Esse é o mais longe que a Júlia consegue chegar do início da prancha sem causar um belo acidente. Então, a faixa de valores que ela consegue ficar é: