Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 65
Um cubo está apoiado em uma parede sem atrito, formando um ângulo θ com o chão, como mostrado na Figura 12-55. Determine o menor coeficiente de atrito estático entre o cubo e o chão, necessário para evitar que o cubo escorregue.
Passo 1
Então gente, para resolver este problema nós temos que colocar as forças que vão atuar neste corpo enquanto ele está apoiado na parede.
Desenhando a situação completa, mas vamos explicando ela aos poucos ao longo da resolução:
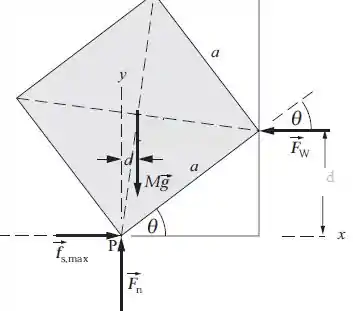
No centro de gravidade, ou seja, no ponto central do cubo, temos a força gravitacional sendo aplicada para baixo. Dada por:
Como nós temos duas superfícies em contato, existe a força normal perpendicular à superfície, que neste caso é o chão, e , força normal entre a parede e o cubo. A força de atrito , no caso da iminência do movimento, é dada por:
Bom, o problema nos disse que o cubo está apoiado na parede, sem escorregar. E nessa situação as condições de equilíbrio são válidas.
Então só precisamos fazer o somatório das forças e dos torques para achar o coeficiente de atrito mínimo para evitar que o corpo escorregue.
Passo 2
Vamos começar usando a primeira condição. Se , então .
Quando observamos as forças, a força peso e a força normal estão sobre o eixo y em direções opostas:
No eixo x estão atuando a força de atrito e a força normal entre a parede e o cubo:
Substituindo
Isolando o coeficiente de atrito:
Passo 3
Para achar a equação da tração vamos usar a segunda condição, . O torque é calculado como:
Onde r é a distância entre a força e o eixo de rotação. A escolha do eixo será muito importante, e será demonstrando em vermelho no desenho abaixo:
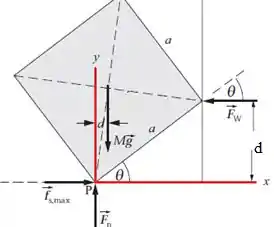
Por que escolhemos este eixo? Eu poderia escolher qualquer ponto para ser a origem, mas se a gente pensar bem, quando colocamos a origem neste ponto nós iremos zerar duas forçar no torque, .
Beleza ! Quando fazemos isso, a força normal da parede estará na posição do eixo de rotação. Como temos a formação de um triângulo retângulo:
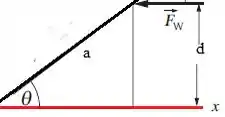
Então, o torque relacionado à é:
Agora temos que achar a distância d entre a força peso e o eixo. Vamos ampliar essa distância da figura original, mas antes é importante a gente lembrar que a diagonal do cubo divide o ângulo (90°) pela metade, ou seja, o ângulo entre a diagonal e as laterais são iguais a 45°:
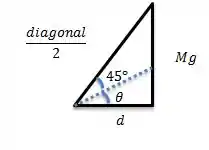
Antes de chegarmos em d, precisamos da diagonal. Como o cubo é formado por dois triângulos retângulos de catetos a, a hipotenusa, ou diagonal, é dada por:
Racionalizando:
Então:
No torque:
Já temos r agora só precisamos saber o sentido de rotação. Por convenção se uma determinada força for capaz de girar o corpo no sentido anti-horário seu sinal será positivo. A força da parede é capaz de girar a barra no sentido anti-horário (+), já a força peso gira no sentido horário (-).
Jogando toda informação na segunda condição:
Isolando
Usando a identidade:
E lembrando que
Na fórmula:
Substituindo no coeficiente: