Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 6.Exercícios e Problemas - Ex. 13

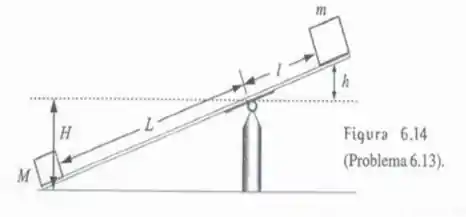
O balanço visto na Figura 6.14 está equilibrado, ou seja, pode ficar estacionário em qualquer inclinação. Portanto, o balanço pode ser levado para a posição horizontal por uma força infinitesimal, cujo trabalho também é infinitesimal. Isto significa que a energia potencial do balanço não se altera quando ele é posto na horizontal. Supondo-se que a tábua tenha massa desprezível, conclui-se então que o aumento de energia potencial do corpo de massa M quando sobe a altura H é igual à diminuição da energia potencial do corpo de massa m quando ele desce a altura h. Use isso para calcular a relação entre M, m, L e l.

Passo 1

Meus grandes gênios!

Para responder essa questão não vamos gastar muito intelecto!

A questão nos garante que:

M g H = m g h

M ∙ H = m ∙ h

Notem um detalhe: o ângulo OPV formado pela balança e o eixo traçado.

Vamos chamar o ângulo de θ .

Sabemos que:

s e n θ = h l ⇒ h = l ∙ s e n ( θ )

E

s e n θ = H L ⇒ H = L ∙ s e n ( θ )

E agora? O que falta? Isso mesmo que vocês pensaram!

M ∙ L ∙ s e n θ = m ∙ l ∙ s e n θ

Por fim:

M . L = m . l

Resposta

m ∙ l = M ∙ L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Por qual fator é alterada a energia cinética de uma partícula se sua rapidez é dobrada mas sua massa é reduzida à metade?
Uma partícula tem, inicialmente, uma energia cinética K. Mais tarde, ela está se movendo no sentido oposto com o triplo de sua rapidez inicial. Qual é, agora, sua energia cinética? (a) K, (b) 3K, (c)
Uma criança cujo peso é 360N balança-se sobre uma piscina usando uma corda presa ao galho de uma árvore na borda da piscina. O galho está a 12m acima do nível do chão, e a superfície da água está a 1,
Um pêndulo consiste de uma corda de comprimento L e uma bolinha de massa m . A molinha é rotacionada até que a bola esteja na horizontal. A bolinha é então projetada para baixo com a rapidez inicial m
A bolinha de um pêndulo de massa m está presa a uma mola leve de comprimento L e também está presa a uma mola com constante de força k . Com o pêndulo na posição mostrada na figura, a mola está no seu