Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 6.Exercícios e Problemas - Ex. 18

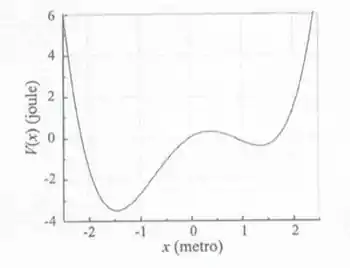
A figura 6.15 mostra a energia potencial de uma partícula, que no SI de unidades é expressa por V x = 1.5 x - 2 x 2 - 0,2 x 3 + 0,5 x 4 . A) Faça um gráfico da força F ( x ) . B) Identifique os pontos de equilíbrio da partícula. C) Quais são os movimentos possíveis da partícula, se sua energia é E = 0 ? D) Indique no gráfico os pontos de retorno da partícula quando sua energia é E = - 2 J .

Passo 1

Salve pessoas, tudo certo? Vamos lá! Primeiro, a questão nos dá a energia potencial:

V x = 1,5   x - 2 x 2 - 0,2 x 3 + 0,5 x 4

Para acharmos a equação da força, basta derivarmos a equação da energia! Logo,

F x = V ' ( x )

F x = 1.5   -   4   x   -   0.6   x 2   +   2   x 3

Passo 2

Os pontos de equilíbrio, são as raízes do gráfico! Logo, temos 3 pontos de equilíbrio!

x 1 = - 1,4443

x 2 = 0,38

x 3 = 1,36343

Passo 3

Para prever os movimentos possíveis da partícula, se a energia E = 0 , é literalmente nenhum. Pois se a energia é 0, e força é 0. Logo, a aceleração é 0.

Passo 4

Para a gente encontrar os pontos de retorno quando a energia é E = - 2 J , precisamos achar a força e a partir daí achar as raízes.

V x = 1,5   x - 2 x 2 - 0,2 x 3 + 0,5 x 4 + 2

F x = 0.5   -   4   x   -   0.6   x 2   +   2   x 3

Pontos:

x 1 = - 1 , 33

x 2 = 0 , 12

x 3 = 1 , 512

Resposta

A ) F x = 1.5   -   4   x   -   0.6   x 2   +   2   x 3

B ) x 1 = - 1,4443

x 2 = 0,38

x 3 = 1,36343

C ) E s t á t i c o

D ) x 1 = - 1,33

x 2 = 0,12

x 3 = 1,512

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de 20k g sobre uma superfície horizontal está preso a uma mola horizontal de constante elástica k = 4,0k N / m . O bloco é puxado para a direita até a mola ficar distendida 10c m em relação a
Uma mola com uma constante elástica de 3200N / m é distendida até que a energia potencial elástica seja 1,44J . ( U = 0 para a mola relaxada.) Quanto é ∆ U se a distensão muda para (a) uma distensão d
Verdadeiro ou falso:(a) A energia total de um sistema näo pode variar. (b) Quando você salta no ar, o chão realiza trabalho sobre você, aumentando sua energia mecânica. (c) Trabalho realizado por forç
Duas pedras são atiradas simultaneamente com a mesma rapidez inicial do teto de um edifício. Uma pedra é atirada a um ângulo de 30º acima da horizontal e a outra é atirada horizontalmente. (Despreze a
Verdadeiro ou falso:(a) A energia total de um sistema näo pode variar. (b) Quando você salta no ar, o chão realiza trabalho sobre você, aumentando sua energia mecânica. (c) Trabalho realizado por forç