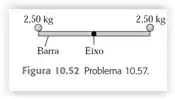
Uma barra delgada e uniforme de e de comprimento possui uma bola muito pequena de grudada em cada extremidade (Figura ). Ela é sustentada horizontalmente por um eixo fino, horizontal e com atrito desprezível, que passa pelo seu centro e é perpendicular à barra. Subitamente, a bola do lado direito se descola e cai, mas a outra permanece grudada na barra.

a) Ache a aceleração angular da barra logo após a bola cair.

b) A aceleração angular permanecerá constante enquanto a barra continua a oscilar? Em caso negativo, ela vai aumentar ou diminuir?

c) Ache a velocidade angular da barra logo após ela oscilar pela sua posição vertical.

1. Vamos começar entendendo a questão: aqui nós temos uma barra com duas bolinhas equilibradas, mas no momento que uma se descola, a barra perde o equilíbrio e começa a girar.

E vamos concordar que ela vai girar com uma aceleração né? E é justamente isso que a letra a nos pede.

Para resolver, precisamos usar a conservação de energia para encontrar a velocidade angular da barra, que oscila na posição vertical.

Para o eixo de rotação, a barra possui . A massa da barra é e o comprimento . Quanto a energia potencial da barra, não sofre alteração.

Para a altura, vamos considerar que (tendo em vista que a bola cai). Calculando o torque:

Para o momento de inércia, temos:

Substituindo em ,

Vamos organizar a expressão que está bem feia e difícil de entender. Reescrevemos o momento de inercia da barra para facilitar a simplificação:

Logo,

Como podemos ver no item (b), outra pergunta que podemos começar a fazer é se a barra cai junto com a bola...

Possivelmente, sim, como podemos perceber na figura, a barra está em equilíbrio, certo?? Se uma das bolas cai, perde-se essa sensação. (Imaginemos uma gangorra, por exemplo)

Assim, quando a bola cai, a barra oscila até o instante que para.

À medida que a barra começa a oscilar, o momento para o peso da bola diminui e a aceleração angular da barra diminui. Portanto, a aceleração não é constante.

Para o item (c), vamos usar a conservação de energia,

No instante inicial, a energia potencial e a energia cinética são iguais a zero, pois não há movimento. Então,

Assim, substituindo os dados, temos:

Isolando a velocidade angular:

Da mesma maneira que fizemos no passo , vamos organizar essa equação:

Agora vai ficar bonitinha, olha só:

Uffa!! É trabalhoso mesmo, mas conseguimos!! Agora podemos substituir os dados:

Prontinho!!