Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 70
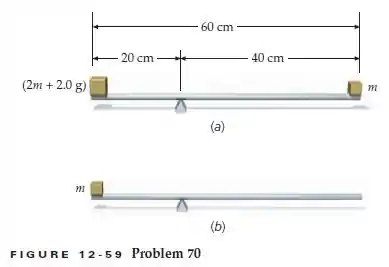
Uma barra fina e homogênea, de 60 cm de comprimento, equilibra-se apoiada a 20 cm de uma das suas extremidades, quando um corpo cuja massa é () está sobre a extremidade mais próxima do ponto de apoio e um corpo de massa m está sobre a extremidade oposta (Figura 12-59a). O equilíbrio é, novamente, alcançado, se o corpo cuja massa é () é substituído pelo corpo de massa m e nenhum outro corpo é colocado na outra extremidade da barra (Figura 12-59b). Determine a massa da barra.
Passo 1
Fala! Então, vamos entender o que está acontecendo com essa barra. A barra suporta o peso das duas massas nas extremidades. Podemos entender que a barra é um corpo extenso.
Falou de corpo extenso, a gente já pensa logo em fazer o diagrama de corpo livre! E como ele fica? Bem, para a primeira situação, onde temos as duas massas, teremos que essas massas vão transmitir seus pesos à barra.
E precisamos lembrar que a própria barra já tem sua massa , ou seja, ela também tem seu peso próprio, que atua no centro de massa da barra, ou seja, na sua metade.
E por que essa barra não cai? Porque temos uma força de reação devido ao apoio. Fazendo um diagrama disso, temos
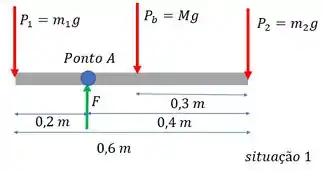
Onde (esse do enunciado significa gramas, a unidade de massa, e o do diagrama que a gente fez é a aceleração da gravidade, tá? Não confunde) e .
E como essa barra está paradinha, podemos usar as equações de equilíbrio
A ideia é a gente usar essas equações na situação 1 (e talvez na 2), para resolver nosso problema. E o que ele quer? Ele quer o valor de , a massa da barra. Vamos!
Passo 2
Cara, podemos começar usando o somatório de torques em relação ao eixo que passa pelo ponto para a situação . Por que?
Não conhecemos a reação em e a força , e nem queremos conhecer. A gente só quer mesmo.
Como a gente tem que está aplicada no ponto , ela não gera momento em relação a esse ponto. Então ela não aparece no somatório de momentos em .
Vamos usar então
Onde os torques são calculados por
Onde r é a distância entre a linha de ação da força e o eixo de rotação. e precisam ser perpendiculares. As distâncias estão descritas na figura. Para , a distância entre sua linha de ação e é , para , temos e para temos
Por convenção, se uma determinada força for capaz de girar o corpo no sentido anti-horário seu sinal será positivo. A força é capaz de girar a barra no sentido anti-horário (+), já a força e a força giram no sentido horário (-). Então nossos torques ficam
Passo 3
Substituindo isso no somatório de torques em relação a :
Lembrando que :
Isolando
Então galera, usando somente a primeira situação já conseguimos achar a massa da barra que era a resposta do problema!