Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 57
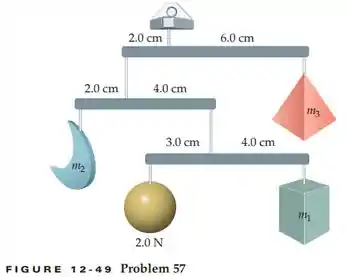
A Figura 12-49 mostra um móbile constituído de quatro objetos pendurados de três barras de massas desprezíveis. Determine os valores das massas desconhecidas dos objetos, sabendo que o móbile está em equilíbrio.
Passo 1
A estretégia nessa questão vai ser começar de baixo pra cima e fazer torque com relação aos pontos de sustentação. Como nosso sistema ta em equilíbrio .
Para o objeto mais baixo, temos:
Logo,
Passo 2
Agora vamos analisar o objeto acima (massa ).
Esse será o peso referente a todo o corpo inferior. Logo,
Isolando :
Fazendo as contas:
Passo 3
Por ultimo, vamos olhar pro objeto lá de cima.
Esse será o peso referente a todo mundo que ta preso ali. Se liga só:
Portanto,
Resposta
Exercícios de Livros Relacionados
A barra horizontal da figura permanece na horizontal se (a) L 1 = L 2 e R 1 = R 2 , (b) M 1 R 1 = M 2 R 2 , (c) M 2 R 1 = M 1 R 2 , (d) L 1 M 1 = L 2 M 2 , (e) R 1 L 1 = R 2 L 2 .
Um pai (massa M ) e seu filho (massa m ) caminham sobre uma gangorra equilibrada, afastando-se para as extremidades opostas. Enquanto eles caminham, a gangorara permanece exatamente na horizontal. O q
Uma bola de boliche padrão pesa 16l i b r a s . Você deseja segurar uma bola de boliche à sua frente, com seu cotovelo dobrado em ângulo reto. Suponha que seu bíceps se prenda a seu antebraço 2,5c m a
Um laboratório de biologia de sua universidade esta estudando a localização do centro de gravidade de uma pessoa em função do seu peso. Eles pagam bem e você se oferece voluntario. A localização do se