Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.11 - Ex. 61

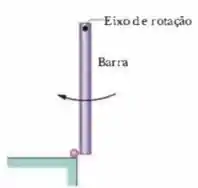
A barra homogênea (de 0,60   m de comprimento e 1,0   k g de massa) da Fig. 11-54 gira no plano do papel em torno de um eixo que passa por uma das extremidades, com um momento de inércia de 0,12   k g ∙ m 2 . Quando a barra passa pela posição mais baixa, colide com uma bola de massa de modelar de 0,20   k g , que fica grudada na extremidade da barra. Se a velocidade angular da barra imediatamente antes da colisão é 2,4   r a d / s , quando é a velocidade angular do sistema barra-massa de modelar imediatamente após a colisão?

Passo 1

Devemos perceber que durante a colisão o momento angular do sistema se converva. Portanto, vamos iniciar esta questão calculando momento de inércia do sistema barra-bola:

I s = I b a r r a + m b o l a r 2

Substituindo os valores, temos:

I s = 0,12 + 0,2 × 0,6 2

I s = 0,192   k g ∙ m 2

Passo 2

Agora, aplicando a lei de conservação do momento angular, temos:

I b a r r a ω b a r r a = I s ω s

Substituindo os valores e isolando ω s :

ω s = 0,12 × 2,4 0,192 = 1,5   r a d / s

Resposta

ω s = 1,5   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas bolas de 2,00k g estão presas às extremidades de uma barra fina de 50,0c m de comprimento e massa desprezível. A barra está livre para girar sem atrito em um plano vertical em torno de um eixo ho
A Fig. 11-59 é uma vista de cima de uma barra fina homogênea de comprimento 0,600m e massa M girando horizontalmente a 80,0r a d / s no sentido anti-horario em torno de um eixo que passa pelo centro.
Na Fig. 11-58, um pequeno bloco de 50g desliza para baixo em uma superfície curva sem atrito a partir de uma altura h = 20c m e depois adere a uma barra homogênea de massa 100g e comprimento 40c m . A
Um parquinho possui um pequeno carrossel com 1,20m de raio e uma massa de 180k g . O raio de giração do carrossel (veja o problema 79 do Capítulo 10) é 91,0c m . Uma criança com 44,0k g de massa corre
Uma partícula de 2,50k g que se move horizontalmente em um piso com velocidade - 3,00m / s j ^ sofre uma colisão perfeitamente inelástica com uma partícula de 4,00k g que se move horizontalmente no me