Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.11 - Ex. 63
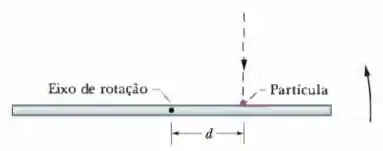
A Fig. 11-59 é uma vista de cima de uma barra fina homogênea de comprimento e massa girando horizontalmente a no sentido anti-horario em torno de um eixo que passa pelo centro. Uma partícula de massa , que se move horizontalmente com uma velocidade de , choca-se com a barra e fica presa. A trajetória da partícula é perpendicular à barra no momento do choque, que ocorre a uma distância do centro da barra. (a) Para que valor de a barra e a partícula permanecem em repouso após o choque? (b) Em que sentido a barra e a partícula giram após o choque se é maior que o valor calculado no item (a)?
Passo 1
Para determinar a distância da barra que a partícula deve bater para parar o sistema, devemos lembrar que na colisão, não há torque resultante, então podemos aplicar a lei de conservação do momento angular. Assim, calculando o momento angular inicial da barra, sabendo que o momento de inércia de uma barra homogênea cujo o eixo de rotação passa pelo seu centro de massa é , então:
Substituindo os valores:
E o momento angular da partícula em relação ao mesmo eixo de rotação:
Substituindo os valores:
Passo 2
Com o momento angular de cada elemento em mãos, devemos perceber que o momento angular da barra aponta para fora da tela, enquanto o momento angular da partícula aponta para dentro da tela (fazer a regra da mão direita, caso não esteja visualizando). Assim:
Como desejamos que o momento angular final seja nulo, aplicando a lei da conservação do momento angular, temos:
Assim, isolando e substituindo o valor de :
Passo 3
Devemos perceber que se , o valor de seria negativo, portanto, o momento angular apontaria no mesmo sentido do momento angular da partícula, ou seja, apontaria para dentro da tela (o sistema iria girar no sentido horário).
Resposta
- ;
- .