Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.11 - Ex. 57

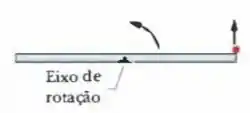
A Fig. 11-52 é uma vista de cima de uma barra fina homogênea, de comprimento 0,800   m e massa M , girando horizontalmente a 20,0   r a d / s , no sentido anti-horário, em torno de um eixo que passa pelo centro. Uma partícula de massa M / 3,00 , inicialmente presa a uma extremidade da barra, é liberada e assume uma trajetória perpendicular à posição da barra no instante em que a partícula foi liberada. Se a velocidade v p da partícula é 6,00   m / s maior que a velocidade da barra imediatamente após a liberação, qual é o valor de v p ?

Passo 1

Primeiro, para iniciar esta questão devemos lembrar que o momento de inércia de uma barra cujo o eixo de rotação passa pelo seu centro de massa como o da figura é:

I b a r r a = 1 12 M L 2

Além disso, devemos perceber que o torque resultante deste sistema é nulo, portanto, pela lei de conservação do momento angular, sabemos que o momento angular antes e depois se conserva.

Passo 2

Aplicando a conservação do momento angular, temos:

I b a r r a ω b a r r a + I b o l a ω b o l a = I b a r r a ω b a r r a ' + m b o l a v b o l a r       e q . 1

Como inicialmente, a bola e a barra estão girando juntos, então ω b a r r a = ω b o l a . Além disso, usando a relação:

ω b a r r a ' = v b a r r a r

E sabendo que v b a r r a = v b o l a - 6 , então, reescrevendo a e q . 1 :

1 12 M ( 0,8 2 ) 20 + M 3 0,8 2 2 20 = 1 12 M 0,8 2 v b o l a - 6 0,4   + M 3 0,8 2 ( v b o l a )

1,067 + 1,067 = 0 , 1 3 3 v b o l a - 6 + 0,133 v b o l a

Isolando v b o l a e substituindo os valores:

v b o l a = 2 × 1,067 + 6 × 0 , 13 3 2 × 0,133

v b o l a = 11,0   m / s

Resposta

v b o l a = 11,0   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Com eixo e raios de massa desprezível e um aro fino, uma certa roda de bicicleta tem raio de 0,35 m e pesa 37 N e pode girar em torno do eixo com atrito desprezível. Um homem segura a roda acima da ca
Se calotas polares de gelo da Terra derretessem totalmente e a água voltasse para os oceanos, estes ficariam cerca de 30 m mais profundos. Que efeito isso teria sobre a rotação da Terra ? Faça uma est
Dois discos estão montados (como um carrossel) no mesmo eixo, com rolamentos de baixo atrito, e podem ser acoplados e girar como se fossem um só disco. O primeiro disco, com um momento de inércia de 3
O rotor de um motor elétrico tem um momento de inércia I m = 2.10 - 3 k g m ² ² em relação ao seu eixo central. O motor é usado para mudar a orientação da sonda espacial no qual está montado. O eixo d
Uma roda está girando livremente com uma velocidade angular de 800 r e v / m i n em torno de um eixo cujo momento de inércia é desprezível. Uma segunda roda, inicialmente em repouso e com momento de i