Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Problemas - Ex. 68

Uma barra metálica de 3,0 N, com 1,50 m de comprimento e resistência de 10,0 Ω, repousa horizontalmente sobre os fios condutores do circuito indicado na Figura 27.62. A barra está em um campo magnético horizontal uniforme de 1,60 T e não está conectada aos fios do circuito. Qual é a aceleração da barra, logo após a chave S ser fechada?

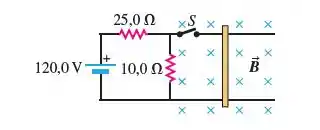
Passo 1

Pelo desenho temos que as únicas forças que atuam no fio são a força magnética e a força peso.

A corrente está na vertical e o campo magnético na horizontal, logo a força magnética está na mesma direção da força peso.

Passo 2

Então pela segunda lei de Newton teremos:

F R = m a

i l B   s e n Φ - m g = m a

Como queremos a aceleração, iremos isolar o a .

a = i l B   s e n Φ - m g m

Como o fio e o campo magnético são perpendiculares s e n   Φ = 1 .

a = i l B   - m g m

Passo 3

Precisamos agora descobrir a corrente.

Pelo desenho, sabemos que a corrente na barra será a metade da corrente total do circuito.

i = I 2

Pela lei de Ohm podemos encontrar a corrente no circuito.

I = V R e q

Passo 4

O resistor de 10 Ω e a barra estão em paralelo, logo a resistência equivalente entre eles será:

1 R = 1 10 + 1 10

R = 5 Ω

Agora, como temos o resistor de 25 Ω   em série com ele, a resistência equivalente total do circuito será:

R e q = = 25 + 5

R e q = 30   Ω

Passo 5

Logo a corrente no circuito será:

I = 120 30

I = 4   A

E a corrente que passa pela barra será:

i = 2   A

Passo 6

Então a aceleração será:

a = 2 ⋅ 1,5 ⋅ 1,6 - 3 3 / 9,8

a = 5,88   m / s 2

Resposta

a = 5,88   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9- Um fio retilíneo transporta uma corrente de 10.0A (Figura 28.35 ). A B C D é um retângulo com um ponto D no meio de um segmento de 1.10m m do fio e um ponto C no fio. Determine o módulo, a direção
14- Uma espira de fio quadrada com 10.0c m em cada lado transporta uma corrente de 15.0A , no sentido horário. Determine o módulo, a direção e o sentido do campo magnético no seu centro em função dos
19- Um fio retilíneo longo está situado sobre o eixo O y e conduz uma corrente I = 8.0A no sentido - O y (Figura 28.39 ). Além do campo magnético produzido pelo fio, existe um campo magnético uniforme
11- Um fio retilíneo está sobre o eixo O z e transporta uma corrente de 4.0A no sentido + z . Determine o módulo, a direção e o sentido do campo magnético prozido por uma segmento do fio de 0.500m m ,
17- ( a ) Quanta corrente um fio longo e retilíneo teria que transportar para que o campo magnético situado a 2.0c m do fio seja igual 1.0G (compável ao campo magnético da Terra, orientado para o nort