Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 23.1 - Ex. 55
Um bastão de comprimento tem carga total uniformemente distribuída ao longo de seu comprimento. O bastão está ao longo do eixo com seu centro na origem. (a) Qual é o potencial elétrico como função da posição ao longo do eixo para ? (b) Mostre que, para , seu resultado se reduz ao devido a uma carga puntiforme
Passo 1
A figura abaixo ilustra o enunciado:
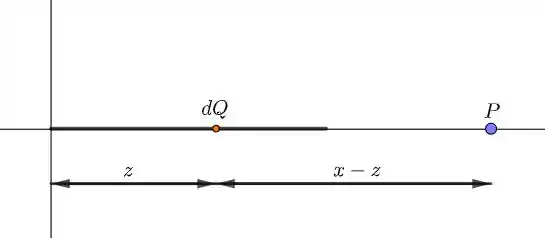
Consideremos um elemento de carga . Assim, o potencial criado por ele é dado por:
Notemos que . Assim,
Passo 2
Integrando, temos que
Vamos mostrar que essa expressão se reduz a de uma carga puntiforme quando . Notemos que podemos escrever
Usando para , segue que
que é o que queríamos mostrar!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A barra fina de plástico da figura abaixo tem um comprimento L = 10,0 cm e uma densidade linear de cargas não uniforme λ = c x , em que c = 49,9 pC/m. (a) Com V = 0 no infinito, determine o potencial
A figura abaixo mostra uma barra fina de plástico de comprimento L = 13,5 cm e uma carga de 43,6 fC uniformemente distribuída.(a) Determine uma expressão para o potencial elétrico no ponto P 1 em funç
A esfera 1, de raio R1, possui uma carga positiva q. A esfera 2, de raio, 2,00R1 , está muito afastada da esfera 1 e inicialmente descarregada. Quando as esferas são ligadas por um fio suficientemente
Qual é a carga em excesso de uma esfera condutora de raio r = 0,15 m se o potencial da esfera é 1500 V e V = 0 no infinito?
A esfera 1, de raio R1, possui uma carga positiva q. A esfera 2, de raio, 2,00R1 , está muito afastada da esfera 1 e inicialmente descarregada. Quando as esferas são ligadas por um fio suficientemente