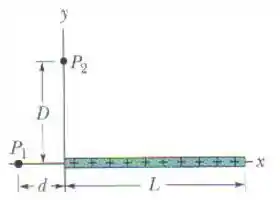
A figura abaixo mostra uma barra fina de plástico de comprimento L = 13,5 cm e uma carga de 43,6 fC uniformemente distribuída.

(a) Determine uma expressão para o potencial elétrico no ponto em função da distância d.

(b) Substitua d pela variável x e determine uma expressão para o módulo da componente do campo elétrico no ponto .

(c) Qual é o sentido de em relação ao sentido positivo do eixo x?

(d) Qual é o valor de no ponto para x = d = 6,20 cm?

(e) Determine o valor de no ponto a partir da simetria da figura.

Letra (b)

Lembra que o campo elétrico é a “derivada” do potencial? Quase isso, na verdade. O certo mesmo é: o campo é menos o gradiente do potencial elétrico. Gradiente lembra derivadas parciais. Como só queremos o campo em x, vamos calcular a derivada parcial só em x:

Mas não temos x no resultado da letra (a), então devemos trocar d por -x. Por que “-x” e não só “x”? Porque d é um valor negativo (está à esquerda). Aí fica assim:

Lembre-se da regra da cadeia:

Mas queremos o módulo do campo

Letra (c)

Na letra (b), logo antes de a gente tirar o módulo, a gente achou um sinal de menos. Então, se a gente pegar um valor positivo de x, o campo vai ficar negativo e, por isso, aponta para o eixo negativo.

Letra (d)

É só pegar a resposta da letra (b) e jogar x = 0,0620 m:

Letra (e)

Pela simetria, a componente vertical é 0. Pensa só: se a componente vertical pudesse ser, por exemplo, para cima, não haveria motivo para não poder ser para baixo, também. As duas possibilidades estão “em pé de igualdade”, por causa da simetria, uma não pode ganhar sobre a outra. A alternativa que sobra é nem um nem outro, ou seja, 0.