Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Exercício - Ex. 25
A bateria de 10,0 V indicada na Figura 26.52 é removida do circuito e reconectada com a sua polaridade invertida, de modo que o terminal positivo fica perto do ponto . O restante do circuito permanece como indicado na figura. Calcule (a) a corrente em cada ramo; (b) a diferença de potencial do ponto em relação ao ponto .
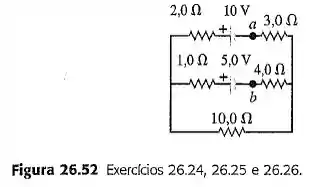
Passo 1
Bom galera, aqui vamos aplicar a regra de junção para reduzir o número de correntes desconhecidas.
Aplicaremos a regra de loop para os dois loops e obter duas equações para as correntes desconhecidas e .
Mas primeiro, vamos esboçar o circuito:
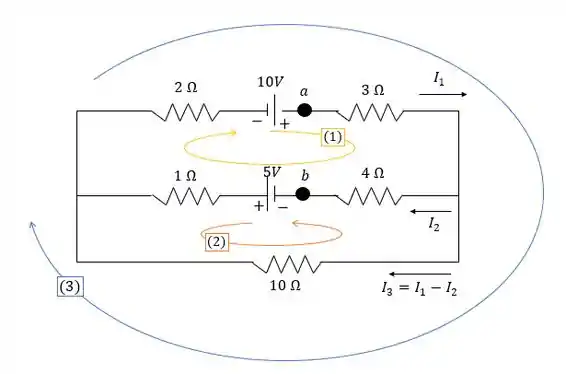
Seja a corrente no resistor de e seja a corrente no resistor de e assuma que essas correntes estão nas direções mostradas. Então a corrente no resistor de é , na direção mostrada, onde usamos a regra dos pontos de Kirchhoff para relacionar a e .
Se obtivermos uma resposta negativa para qualquer uma dessas correntes sabemos que a corrente está realmente na direção oposta à que assumimos. Três voltas s instruções para percorrer os loops são mostradas no diagrama do circuito. Aplique a regra de loop de Kirchhoffs a cada loop.
Passo 2
-
Loop (1):
Passo 3
Loop(2):
Passo 4
A primeira equação nos diz
Usando a segunda equação:
Então,
Passo 5
- Para encontrar :
comece no ponto e vá para o ponto . Muitas rotas diferentes podem de a e todos devem produzir o mesmo resultado para .
Viaje pelo resistor de e depois pelo resistor de :
(o ponto tem maior potencial que o ponto )
Resposta
- ; ; .