Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 7.Problemas - Ex. 23
Um bloco de 200 g é pressionado contra uma mola de constante elástica de 1,40 kN/m até comprimi-la 10,0 cm. A mola repousa na base de uma rampa inclinada a 60,0º com a horizontal. Usando considerações de energia, determine que distância o bloco se move para cima na inclinação a partir de sua posição inicial antes de parar (a) se a rampa não exerce força de atrito sobre o bloco e (b) se o coeficiente de atrito cinético é 0,400.
Passo 1
Vamos primeiro ver um esboço da situação:
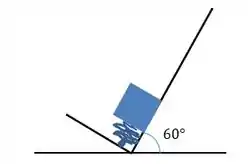
(a)Desconsiderando o atrito, a gente pode dizer que toda a energia potencial elástica na mola vai se converter em energia potencial gravitacional pro bloco quando a mola for solta, sem perdas de energia, certo?
Vamos escrever isso matematicamente:
Aplicando os dados que a gente conhece, observando as unidades sempre, e considerando , vamos ter o seguinte:
Esse é o valor da altura atingida verticalmente pelo bloco na subida pela rampa.
Se a gente quer saber a distância que ele percorreu na rampa em si, precisamos usar um pouco de trigonometria. A situação é essa:
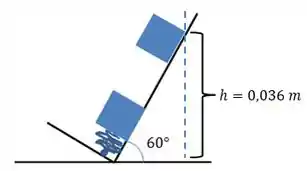
A gente tem esse triângulo retângulo na figura formado pela rampa (hipotenusa), pelo chão e pela altura atingida pelo bloco (catetos).
Sabendo o ângulo entre a rampa e o chão, a gente pode usar o seno do ângulo pra determinar o tamanho da hipotenusa! A gente tem:
Isolando , temos:
Passo 2
(b)Agora, a gente faz a mesma coisa, só que uma parte da energia potencial elástica da mola, ao ser transferida pro bloco, é perdida por atrito.
Então precisamos descontar a parcela do trabalho da força de atrito, , da energia potencial elástica inicial. A gente escreve isso aqui:
Sendo a formulinha pro trabalho do atrito , onde é o deslocamento total do bloco e é a força de atrito (sendo ), a gente tem:
Bom, antes de seguir, a gente precisa saber quem é a força normal . Pra isso, vamos usar um pouco de decomposição de vetores. Olha esse esqueminha:
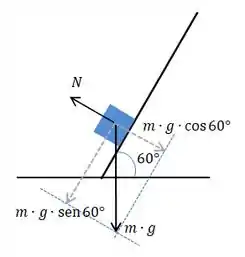
As setinhas pontilhadas são as decomposições do vetor força peso do bloco, tomando como referência a inclinação da rampa.
Pensa comigo: se o bloco não “afunda” na rampa e nem flutua a partir da rampa, é porque, necessariamente, e são iguais em módulo, e se cancelam!
Com isso a gente consegue substituir por na última expressão que escrevemos! A gente fica assim:
Mas, ainda tem um probleminha: a gente ficaria com duas incógnitas: e . Mas resolver isso é fácil, uma vez que essas medidas se correlacionam por um triângulo retângulo como a gente viu no Passo 1. Assim, a relação entre e vale:
Maravilha? Agora a gente substitui por essa expressão na equação maior e vamos determinar !
Passo 3
Ficamos assim:
Vamos passar pro outro lado da igualdade e colocar o que for possível em evidência:
Agora, vamos isolar em um lado da igualdade e inserir os dados que a gente tem!
Jogando esse monstrinho na calculadora, a gente resulta em:
Assim a gente verifica que, realmente, a distância alcançada foi menor, já que parte da energia potencial elástica foi perdida na forma de calor pelo atrito!
Resposta
(a)
(b)