Um professor de física encontra-se em pé, em repouso, sobre uma plataforma giratória de e de diâmetro capaz de girar sem atrito. Seu ajudante possui uma roda de bicicleta com de diâmetro à qual de pedaços de chumbo foram presos ao aro. Existe um mancal de cada lado do eixo da roda, de modo que se pode segurá-la enquanto ela gira. O ajudante põe a roda a girar a e a mantém girando em um plano horizontal (a rotação se dá em torno de um eixo vertical) tal que a rotação se dá em sentido anti-horário quando vista a partir do teto da sala de aula. Ele, então, entrega a roda girando ao professor.

Quando o professor pega a roda pelos mancais laterais e o assistente a solta, algo acontece com o professor? Em caso afirmativo, descreva o movimento do professor e calcule quaisquer grandezas que sejam relevantes. Em caso negativo, explique por que não.

Agora o professor gira o eixo da roda em , de modo que o mancal, que antes estava em cima da roda, passa agora a estar embaixo da mesma. Algo acontece com o professor? Em caso afirmativo, descreva o movimento do professor e calcule quaisquer grandezas que sejam relevantes. Em caso negativo, explique por que não.

Sugestão: você precisará usar modelos para tratar tanto o professor quanto a roda. O professor tem uma massa total de . Suas pernas e seu tronco somam . Eles possuem um diâmetro médio de e uma altura de . Os braços dele são de cada, e ele segura a roda mantendo os mancais a do centro de seu corpo. Não esqueça de que a roda tanto gira quanto se desloca junto com o professor.

Letra

Como o momento angular total inicial e final deve ser igual professor deve adquirir algum momento angular. Vamos determinar a frequência, ela é uma grandeza importante.

O momento angular inicial é:

Lembre da :

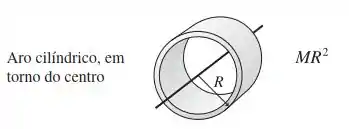
Quando ela é posta de cabeça para baixo:

Como no sistema o momento angular total inicial e final deve ser igual:

Agora calcular a velocidade angular da plataforma giratória usando:

Onde

Desenvolvendo cada um:

Finalmente podemos encontrar , fazendo: