Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 40

Princípios Da Física – Serway – Vol.1 – 5ª Ed., Cap.10, Problemas, Questão 40

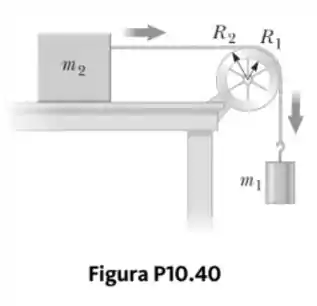
Na Figura P10.40, o corpo pendurado tem massa de m 1   =   0,420   k g ; o bloco deslizante tem massa de m 2   =   0,850   k g ; e a roldana é um cilindro oco com massa de M   =   0,350   k g , raio interno R 1   =   0,020   0 e raio externo R 2   =   0,030   0   m . Suponha que a massa dos raios seja desprezível. O coeficiente de atrito cinético entre o bloco e a superfície horizontal é μ k   =   0,250 . A roldana gira sem atrito sobre seu eixo. Uma corda leve não estica nem escorrega na roldana. O bloco tem velocidade de v i   =   0,820   m / s na direção da roldana quando passa por um ponto de referência na mesa.

  1. Use métodos de energia para prever sua velocidade após ter se movido para um segundo ponto 0,700   m distante.
  2. Encontre a velocidade angular da roldana no mesmo momento.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

Aplique Δ K + Δ U + Δ E int  = 0

Onde,

Δ E int  = f k d

μ = 0.250

f k = μ n 2 = μ m 2 g

As energias cinética translacional e rotacional estão presentes no sistema. Temos também v i = 0.820 m s . Encontre v . A velocidade angular da polia é ω i = v i R 2 ,   e   ω = v R 2 . A massa m 1 passa por h = d quando a massa m 2 move a distância d = 0.700 m .

I = 1 2 M R 1 2 + R 2 2

Onde R 1 = 0.0200 m , R 2 = 0.0300 m ,   e   M = 0.350 k g , então:

K f - K i + U f - U f + Δ E int  = 0 1 2 m 2 v 2 - 1 2 m 2 v i 2 + 1 2 m 1 v 2 - 1 2 m 1 v i 2 + 1 2 I ω 2 - 1 2 I ω i 2 + m 1 g y - m 1 g y i + f k d = 0

1 2 m 1 + m 2 v 2 - v i 2 + 1 2 I v R 2 2 - v i R 2 2 + m 1 g y - y i + μ m 2 g d = 0

1 2 m 1 + m 2 v 2 - v i 2 + 1 2 1 2 M R 1 2 + R 2 2 1 R 2 2 v 2 - v i 2 + m 1 g - d + μ m 2 g d = 0

1 2 m 1 + m 2 v 2 - v i 2 + 1 2 1 2 M 1 + R 1 2 R 2 2 v 2 - v i 2 = g d m 1 - μ m 2

1 2 m 1 + m 2 + 1 2 M 1 + R 1 2 R 2 2 v 2 - v i 2 = g d m 1 - μ m 2

v = v i 2 + 4 g d m 1 - μ k m 2 2 m 1 + m 2 + M 1 + R 1 2 R 2 2 1 2

v = ( 0.820 ) 2 + 4 9.80 0.700 0.420 - 0.250 0.850 2 0.420 + 0.850 + 0.350 1 + ( 0.0200 ) 2 ( 0.0300 ) 2 1 2

= 1.59 m s

Passo 2

Letra b:

ω = v r = 1.59 m s 0.0300 m = 53.1 r a d s

Resposta

  1. 1.59 m s
  2. 53.1 r a d s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para ligar um cortador de grama, você deve puxar uma cordinha que está enrolada ao longo do perímetro de um volante. Depois de você puxar a corda por 0,95 s , o volante está girando a 4,5 revoluções p
Uma roda tem um aro fino de 3,0 k g e quatro raios, cada um com 1,2 k g de massa. Determine a energia cinética da roda quando rola a 6,0 m / s sobre uma superfície horizontal.
Determine a aceleração angular do cilindro do problema 96. Ele gira no sentido horário ou anti-horário? (b) Qual é a aceleração linear do cilindro (magnitude e orientação) em relação à mesa? (c) Qual
Como engenheiro-chefe de projetos de uma grande fábrica de brinquedos, você deve projetar um brinquedo tipo montanha-russa. A idéia, como mostrada na figura, é que a bolinha de massa m e raio r deve d
Se a força do problema 96 atua ao longo de uma distância d , forneça, em termos dos símbolos, (a) a energia cinética da barra e (b) a energia cinética total do cilindro. (c) Mostre que a energia cinét