Um bloco de aço de encontra-se em repouso sobre uma mesa de aço. Um barbante horizontal puxa o bloco.
- Qual é o mínimo valor da tensão no barbante para que o bloco comece a escorregar?
- Se a tensão no barbante for de , qual será o módulo da velocidade do bloco após ter se deslocado ?
- Se a tensão no barbante for de e a mesa estiver coberta por óleo, qual será o módulo da velocidade do bloco após ter se deslocado ?
Passo 1
Primeiro de tudo vamos fazer o que??
Isso aí mesmo! Diagrama de corpo livre.
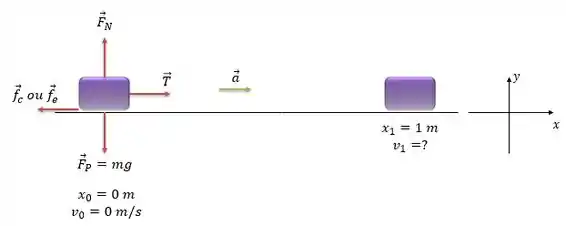
As forças que atuam no bloco são a força peso e a força normal na direção e na direção temos a tensão na corda que puxa o bloco e a força de atrito do bloco com a mesa. Essa força de atrito pode ser atrito estático, enquanto o bloco está parrado ou atrito cinético, quando o bloco passa a ter movimento, show de bola?
Na Tabela 6.1 do livro você encontra os valores dos coeficientes de atrito cinético e estático para o aço sobre aço:
Passo 2
- Qual é o mínimo valor da tensão no barbante para que o bloco comece a escorregar?
- Se a tensão no barbante for de , qual será o módulo da velocidade do bloco após ter se deslocado ?
- Se a tensão no barbante for de e a mesa estiver coberta por óleo, qual será o módulo da velocidade do bloco após ter se deslocado ?
Quando temos um objeto parado sobre uma superfície e queremos tirar ele do repouso a força que devemos fazer deve ser NO MÍNIMO igual em módulo a força de atrito estático que a superfície exerce sobe o objeto.
Então:
A força de atrito estático é dada por:
Precisamos achar o módulo da força normal. O bloco não se movimenta na direção e por isso o somatório das forças nessa direção tem que ser zero:
Logo:
E:
Sabendo que:
Temos:
Passo 3
Aplicando a segunda Lei de Newton na direção , para acharmos a aceleração do bloco:
Note que nesse caso, a força de atrito é a força de atrito cinético, porque o bloco está em movimento, belezinha?
A força de atrito cinético é dada por:
Então:
Conhecendo:
Temos:
Passo 4
Tendo a aceleração conhecida vamos aplicar a equação de Torricelli para achar a velocidade, .
Temos que:
Logo:
Passo 5
Para resolver vamos fazer os mesmos passos que fizemos para a letra b, MAS aqui utilizaremos outro coeficiente de atrito cinético, porque agora a mesa está coberta de óleo, sacou?
Na Tabela 6.1 do livro você encontra que o valor do coeficiente de atrito cinético para o aço sobre aço, com lubrificação, como óleo, é:
Achando a aceleração, utilizando a fórmula que encontramos na letra b, através da segunda lei de Newton:
Achando a velocidade, , pela equação de Torricelli:
Ufaa! Acabamos =)