Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 44
Você e seu amigo Peter estão pondo novas telhas de madeira em um telhado com de inclinação. Você está sentado bem no topo do telhado quando Peter, na beira do telhado abaixo de onde você se encontra, a de distância, pede-lhe para alcançar uma caixa de pregos. Em vez de levar a caixa de de pregos até Peter, você decide dar um pequeno empurrão na caixa para fazê-la deslizar até ele. Se o coeficiente de atrito cinético entre a caixa e o telhado é de , que valor de velocidade você deve imprimir à caixa a fim de que ela chegue suavemente e pare bem próximo à borda do telhado?
Passo 1
Vamos analisar a situação da caixa de pregos deslizando do topo do telhado até a beira, mostrando as forças que atuam:
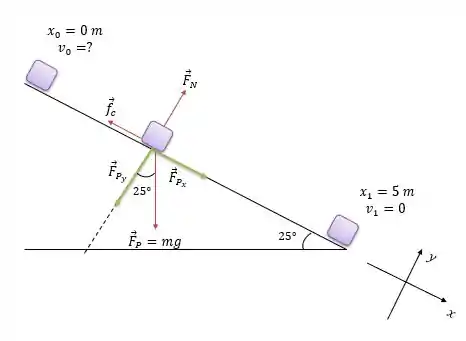
De acordo com o sistema de coordenadas adotado, podemos decompor a força peso em uma componente e outra componente :
Sempre lembrando: COlado – COsseno; SEparado – SEno
Passo 2
A caixa não se movimenta na direção , então:
Passo 3
Podemos aplicar, na direção , a segunda lei de Newton para acharmos aceleração adquirida pela caixa de pregos:
O módulo da força de atrito pode ser escrito como:
Substituindo a força normal encontrada anteriormente:
Substituindo a força de atrito na equação para aceleração, temos:
Tendo:
Conseguimos calcular a aceleração:
Passo 4
Tendo a aceleração, utilizamos a equação de Torricelli para acharmos a velocidade inicial necessária:
Temos que a velocidade final tem que ser zero:
E a distância percorrida é o comprimento da telha:
Então: