Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 35
Uma vítima de acidente que quebrou a perna está imobilizada numa cama com sua perna mantida suspensa e tensionada. O paciente calça uma bota especial presa a um cabo que passa por uma polia. O pé e a bota possuem uma massa conjunta de , e o médico decidiu usar uma massa de presa na extremidade do cabo. A bota, então, é mantida suspensa pelo cabo e não toca a cama.
- Usando a primeira lei de Newton para analisar a massa suspensa, determine o valor de tensão no cabo.
- A força de tração resultante precisa puxar a perna horizontalmente para a frente. Qual é o valor apropriado do ângulo da parte superior do cabo?
- Qual é o valor da força de tração resultante sobre a perna?
Sugestão: se as polias não têm atrito, como consideramos aqui, a tensão no cabo é constante de uma extremidade a outra.
Passo 1
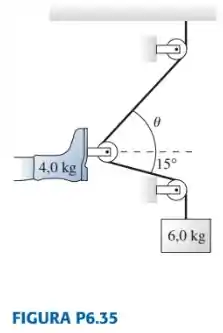
Nosso primeiro passo vai ser desenhar todas as força de atuam no pé do paciente e no bloco de massa:
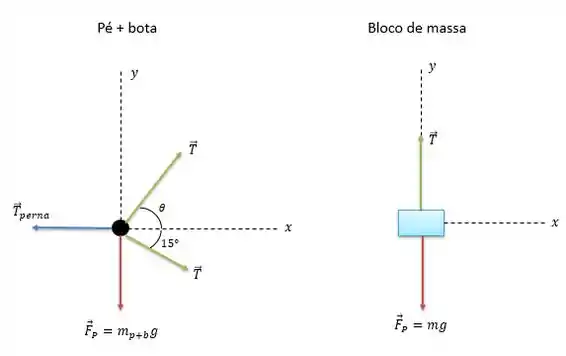
As força que atuam no pé do paciente são as duas tensões na sessão inferior e superior do cabo, a força peso e a tensão feita pela própria perna do paciente.
Já as forças que atuam no bloco de massa são a tensão no cabo e a força peso.
Note que que estamos considerando que as polias não possuem atrito e por isso as tensões no cabo são as mesmas
Passo 2
- Usando a primeira lei de Newton para analisar a massa suspensa, determine o valor de tensão no cabo.
- A força de tração resultante precisa puxar a perna horizontalmente para a frente. Qual é o valor apropriado do ângulo da parte superior do cabo?
- Qual é o valor da força de tração resultante sobre a perna?
Vamos olhar só para o diagrama de corpo livre do bloco de massa. Esse bloco está em equilíbrio, então o somatório de forças que atuam sobre o bloco precisa ser zero.
A massa do bloco foi fornecida na questão e a aceleração da gravidade tem um valor conhecido:
Então:
Passo 3
Agora, vamos olhar para o diagrama de corpo livro do pé do paciente. Podemos decompor as tensões na corda em componentes na direção e na direção :
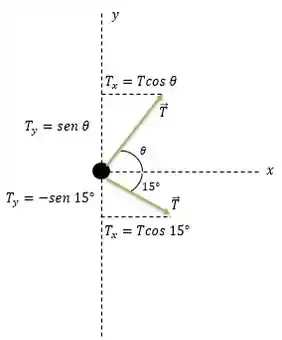
Sempre lembrando: colada – cosseno, separada – seno
O pé do paciente também está em equilíbrio e o somatório das forças em nas duas direções e tem que ser zero. Nesse momento, vamos olhar para a direção :
A massa do conjunto pé mais bota foi dado na questão:
O valor da tensão nós achamos na letra a:
E:
Então:
Agora, para sabermos o ângulo precisamos fazer o inverso da função seno:
Passo 4
Agora, vamos olhar para a direção :
Temos que:
E a tensão na corda nós já calculamos:
Logo:
Matamos a questão =)