Um bloco cúbico com densidade e a aresta de comprimento flutua sobre um liquido de densidade maior . a) Que fração do volume do bloco fica acima da superfície do liquido? b) O liquido é mais denso do que a água (densidade igual a e não se mistura com ela. Derramando-se água sobre a superfície do liquido, qual deve ser a camada da água para que a superfície livre da água coincida com a superfície superior do bloco? Expresse a resposta em termos de . e . c) Calcule a profundidade da camada de água da parte (b) se o liquido for mercúrio e o bloco for aço com aresta de q0,0 cm.
Passo 1
Aplicaremos a segunda lei de Newton ao bloco. Na parte (a), usaremos o princípio de Arquimedes para a força de flutuação. Na parte (b), usaremos a equação
para encontrar a pressão na face inferior do bloco e, em seguida, usar a equação
para calcular a força que o fluido exerce.
Passo 2
- Vamos esboçar um diagrama de corpo livre para o bloco
- Deixe a camada de água ter profundidade. Vamos esboçar a situação:
- E então
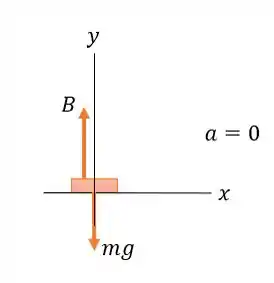
Assim,
Isso implica que
A fração do volume submerso é .
Assim, a fração que está acima da superfície é .
Se , o bloco fica totalmente submerso à medida que flutua.
Passo 3
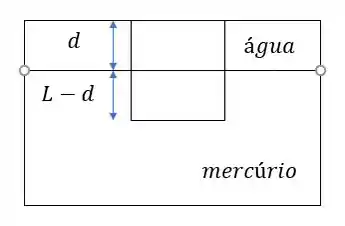
Então,
Aplicando ao bloco, temos que:
e se dividem e
Isso implica que
Passo 4
Na expressão derivada na parte (b), se o bloco flutua no líquido totalmente submerso e nenhuma água precisa ser adicionada. Se o bloco continua a flutuar com uma fração acima da água, é adicionada água e a água nunca chega ao topo do bloco ().