Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Problemas - Ex. 92

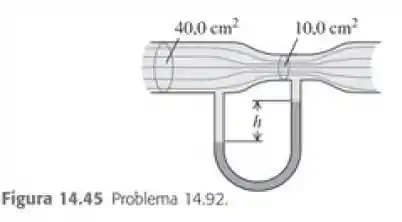
O tubo horizontal mostrado na Figura 14.45 apresenta seção reta com área igual a 40,0 c m 2 em sua parte mais larga e 10,0 c m 2 em sua constrição. A água flui no tubo, e a vazão volumétrica é igual a 6,0 × 10 - 3   m 3 / s   ( 6,0 L / s ) . Calcule a) a velocidade do escoamento na parte mais larga e na constrição; b) a diferença de pressão entre essas duas partes; c) a diferença de altura entre os dois niveis do mercurio existente no tubo em U.

Passo 1

Vamos aplicar a equação de Bernoulli aos pontos 1 e 2. Aplicaremos p = p 0 + ρ g h   aos dois braços do tubo em forma de U para calcular h .

A taxa de descarga é

v 1 A 1 = v 2 A 2

A densidade do mercúrio é ρ = 13,6 × 10 3 k g / m 3

E a densidade da água é 1,000 × 10 3 k g / m 3

Seja o ponto 1 onde A 1 = 40 × 10 - 4 m 2 e o ponto 2 é onde A 2 = 10 × 10 - 4 m 2

E y 1 = y 2

Passo 2

  1. Então, a velocidade do escoamento na parte mais larga e na constrição é dada, respectivaente, por

    2. v 1 = 6,00 × 10 - 3 k g / m 3 40,0 × 10 - 4 m 2 = 1,50   m / s

    E

    v 2 = 6,00 × 10 - 3 k g / m 3 1 0,0 × 10 - 4 m 2 = 6,0 0   m / s

    Passo 3

  2. E calculamos a diferença de pressão por

    3. p 1 + ρ g y 1 + 1 2 ρ v 1 2 = p 2 + ρ g y 2 + 1 2 ρ v 2 2

    p 1 p 2 = 1 2 ρ v 2 2 - v 1 2 = 1 2 1000 k g m 3 6 m s 2 - 1,50 m s 2 = 1,69 × 10 4   P a  

    Passo 4

  3. E a diferença entre as alturas dos níveis:

p 1 + ρ w g h = p 2 + ρ m g h

Isso implica que

h = p 1 - p 2 ρ m = ρ w g = 1,69 × 10 4 P a 13,6 × 10 3 k g m 3 - 1,00 × 10 3 k g m 3 ( 9,8 m s 2 ) = 0,137   m = 13,7   c m

A pressão no fluido diminui quando a velocidade do fluido aumenta.

Resposta

  1. v 1 = 1,50   m / s e v 2 = 6,00   m / s
  2. 1,69 × 10 4   P a
  3. 13,7   c m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque de água encontra-se sobre um carinho que pode mover-se sobre um trilho horizontal com atrito desprezível. Há um pequeno orifício numa parede, a uma profunidade h abaixo do nível da água no t
Um modelo aproximado da câmara de combustão de um foguete é um recipiente contendo gás que se mantém a uma pressão constante p , com um orifício pelo qual o gás escapa para o exterior, onde a pressão
Um tubo contendo ar comprimido a uma pressão de 1,25a t m tem um vazamento através de um pequeno orifício em sua parede lateral. Sabendo que a densidade do ar na atmosfera é de 1,3k g / m 3 , calcule
Um filete de água escorre verticalmente de uma torneira de raio a , com o escoamento estacionário de vazão Q . Ache a forma do jato de água que cai, determinando o raio ρ da secção transversal em funç
Um avião tem uma massa total de 2.000k g e a área total coberta por suas asas é de 30m 2 . O desenho de suas asas é tal que a velocidade de escoamento acima delas é 1,25 vezes maior que abaixo, quando