Enunciado
Física - Serway e Jewett - Física para cientistas e engenheiros - Vol1 - Ed: 1º - Capítulo 5.Problemas - Ex. 21c
Um bloco desliza para baixo em um plano sem atrito com uma inclinação de . O bloco parte do repouso no topo e o comprimento da rampa é de .
- Desenhe um diagrama de corpo livre do bloco. Encontre
- a aceleração do bloco e
- sua velocidade quando ele atinge a parte inferior da rampa.
Passo 1
E aiii galera, vamos fazer uma questão aqui?
Vem comigo!
Letra a:
Abaixo, temos o esquema do diagrama de corpo livre:
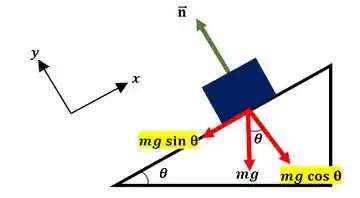
Passo 2
Letra b:
Como podemos encontrar uma força líquida e queremos uma aceleração, este problema é categorizado como um problema que pode ser resolvido pela segunda lei de Newton que aplicamos na direção x:
Passo 3
Letra c:
Como a aceleração é constante, podemos usar a seguinte equação de partícula sob aceleração constante:
Resposta
- Ver diagrama
Exercícios de Livros Relacionados
Um esquiador de 40k g desce uma rampa sem atrito que faz um ângulo de 10 ° com a horizontal. Suponha que o esquiador se desloca no sentido negativo de um eixo x orientado ao longo da rampa. O vento ex
Um esquiador de 50k g é puxado para o alto de uma encosta sem atrito segurando um cabo que se move paralelamente à encosta, que faz um ângulo de 8,0 ° com a horizontal. Qual é o módulo F c a b o da fo
Uma caixa com uma massa de 5,00k g sobe uma rampa sem atrito que faz um ângulo θ com a horizontal. A Fig. 5-41 mostra, em função do tempo t , a componente v x , da velocidade da caixa ao longo de um e
No arremesso de peso, muitos atletas preferem lançar o peso com um ângulo menor que o ângulo teórico (cerca de 42 ° ) para o qual a distância é máxima para um peso arremessado com a mesma velocidade e
A Fig. 5-56 mostra uma caixa de massa m 2 = 1,0k g sobre um plano inclinado sem atrito de ângulo θ = 30 ° . Ela está ligada por uma corda de massa desprezível a uma caixa de massa m 1 = 3,0k g sobre u