Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 36
Um esquiador de desce uma rampa sem atrito que faz um ângulo de com a horizontal. Suponha que o esquiador se desloca no sentido negativo de um eixo orientado ao longo da rampa. O vento exerce uma força sobre o esquiador de componente . Quanto vale , se o módulo da velocidade do esquiador (a) é constante, (b) aumenta a uma taxa de e (c) aumenta a uma taxa de ?
Passo 1
Para iniciar essa questão precisamos ter em mente que a força resultante que age sobre um corpo é a soma de todas as forças que atuam no mesmo e está relacionada à aceleração pela definição da segunda lei de Newton:
Lembrando que podemos aplicar a segunda lei de Newton para cada componente:
O problema nos dá a massa do esquiador (), o ângulo que a rampa faz com a horizontal (), fala que o vento exerce sobre o esquiador uma força e pede para determinarmos esta força em três situações (, e ).
Passo 2
Inicialmente, vamos fazer um diagrama do corpo livre:
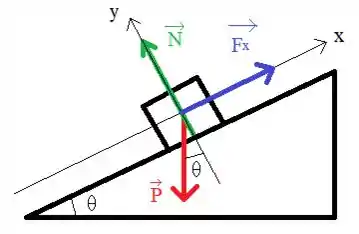
Com essa ilustração, conseguimos visualizar melhor como as forças estão agindo de acordo com os eixos, certo?
Vamos escrever a segunda lei de Newton para o eixo , lembrando que o esquiador está descendo:
Substituindo os valores:
Isolando :
Passo 3
Substituindo os valores dado no enunciado. Primeiro, :
Passo 4
Para , faremos de maneira análoga:
Passo 5
Para :
Resposta
- ;
- ;
- .