Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 5.Problemas - Ex. 7

Um bloco é lançado para cima, com velocidade de 5 m/s, sobre uma rampa de 45 ° de inclinação. O coeficiente de atrito cinético entre o bloco e a rampa é de 0,3. a) Qual é a distância máxima atingida pelo bloco ao longo da rampa? b) Quanto tempo leva o bloco para subir a rampa? c) Quanto tempo leva para descer a rampa? d) Com que velocidade final chega ao pé da rampa?

Passo 1

Vamos começar entendendo o problema pelo seu diagrama

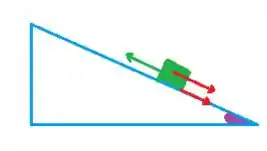
(O ângulo roxo vai ser nosso θ = 45 ° )

Os dois vetores vermelhos são das forças peso e atrito que atuam no corpo, já o vetor verde corresponde à velocidade inicial do corpo. Sabendo que o Peso que atua é m g s e n θ vamos aplicar nossa lei de newton!

F r e s = - ( m g s e n θ + μ c N )

Galera, um detalhe aqui, como saberemos o valor da normal?

Basta a gente olhar se o bloco ta saindo flutuando do plano inclinado ou afundando nele. Já da pra ver que não né? Haha, por isso nossas componentes na perpendicular do plano se anulam, beleza?

Como as componentes na perpendicular são   N   e   m g c o s θ , então para o movimento subindo o plano,

F r e s = - ( m g s e n θ + μ c m g c o s θ )

→

a r e s =   - g   s e n θ + μ c c o s θ

=   - 9,8 1 2 + 0,3   2 =   - 9   m / s 2  

Show! Só mais uma coisa, quando o bloquinho estiver descendo ao invés de ter os 2 vetores apontando pra baixo a gente só vai ter a gravidade fazendo isso, o atrito vai estar pra trás, porque sempre é contrário à velocidade, então a gente fica com isso ó

a r e s =   g   s e n θ - μ c c o s θ

= - 9,8 1 2 - 0,3   2 = 4,85   m / s 2

Passo 2

  1. A distância máxima é percorrida quando a velocidade final chega a 0. Usando torricelli fica asism

    2. Δ s = ( v 2 - v o 2 ) 2 a r e s

    →

    Δ s = - v o 2 - 2 g (   s e n θ + μ c c o s θ )

    = 5 2 2 .   9

    = 1,39   m

    Passo 3

  2. O tempo para subir calcularemos assim

    3. v = v 0 + a t

    →

    0 = 5 - 9 t

    t = 5 9 = 0,56   s

    Passo 4

  3. Para descer temos

    4. Δ s = ( v 2 - v o 2 ) 2 a r e s

    Onde v 0 = 0   ,     Δ s = 1,39   m  

    →

    v = 2   .   Δ s   .     a r e s  

    = 2   .   1,39   .   4,85 = 3,67   m / s  

    Já que v = v 0 + a t

    →

    3,67 = 4,85   t

    →

    t = 3,67 4,85 = 0,76   s

  4. Como já respondido v = 3,67   m / s

Resposta

a )   1,39   m

b )   0,56   s

c )   0,76 s

d )   3,67   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um estudante, enlouquecido pelos exames finais, usa uma forçaP de módulo 80N e ângulo θ=70 ° para empurrar um bloco de 5,0k g no teto do quarto (Fig. 6-52). Se o coeficiente de atrito cinético entre o
Na Fig. 6-51, um caixote escorrega para baixo em uma vala inclinada cujos lados fazem um ângulo reto. O coeficiente de atrito cinético entre o caixote e a vala é μ k . Qual é a aceleração do caixote e
Na Fig. 6-59, o bloco 1 de massa m 1=2,0k g e o bloco 2 de massa m 2=1,0k g estão ligados por um fio de massa desprezível. O bloco 2 é empurrado por uma força F de módulo 20N que faz um ângulo θ=35 °
O bloco A da Fig. 6-56 possui massa m a=4,0k g e o bloco B possui massa m b=2,0k g . O coeficiente de atrito cinético entre o blocoB e o plano horizontal é μ k=0,50 . O ângulo do plano inclinado sem a
Uma cômoda com uma massa de 45k g , incluindo as gavetas e as roupas, está em repouso sobre o piso. (a) Se o coeficiente de atrito estático entre a cômoda e o piso é 0,45 , qual é o módulo da menor fo