Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 81

O bloco A da Fig. 6-56 possui massa m a   =   4,0   k g e o bloco B possui massa m b   =   2,0   k g . O coeficiente de atrito cinético entre o bloco   B e o plano horizontal é μ k   =   0,50 . O ângulo do plano inclinado sem atrito é θ = 30 ° . A polia serve apenas para mudar a direçãodo fio que liga os blocos. O fio possui massa desprezível. Determine :

(a)a tensão do fio e (b) o módulo da aceleração dos blocos .

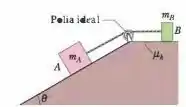
Passo 1

Opa!! Vamos começar dando uma olhada nos diagramas de corpo livre para entendermos melhor o problema:

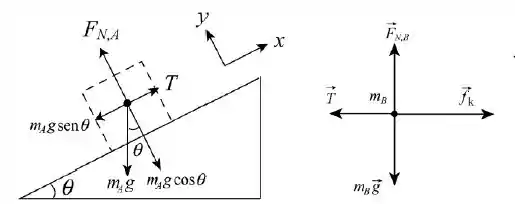
Agora podemos aplicar a Segunda Lei de Newton ao bloco A e ao bloco B.

Bloco A

m a g sen ⁡ θ - T = m a a

Bloco B

T - f k = m b a

Beleza?!

Nós sabemos que a força de atrito é dada por   f k = μ k F N , B . Podemos substituir f k por seu valor na segunda equação, obtemos assim um sistema de equações que pode ser resolvido para obter os valores da tensão T e da aceleração a .

Resolvendo o sistema de equações, obtemos:

T = m a m b m a + m b sen ⁡ θ + μ k g = 4 k g 2 k g 4 k g + 2 k g sen ⁡ 30 °   + 0,50 9,8 m s 2 = 13 N

Passo 2

Agora só falta encontrarmos a aceleração que pode ser obtida através da relação

a = m a sen ⁡ θ - μ k m b m a + m b g

Assim,

a = 4 k g sen ⁡ 30 ° - 0,5 2 k g 4 k g + 2 k g 9,8 m s 2 = 1,6 m / s 2

Resposta

T = 13 N

a = 1,6 m / s 2

Tranquilo pessoal??? Bora resolver mais questões então!!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 6-33, dois blocos estão ligados por um fio que passa por uma polia. A massa do bloco A é 10k g e o coeficiente de atrito cinético entre A e a rampa é 0,20 . O ângulo θ da rampa é 30 ° . O bloc
Você depõe como perito em um caso envolvendo um acidente no qual o carro A bateu na traseira de um carro B que estava parado em um sinal vermelho no meio de uma ladeira (Fig. 6-25). Você descobre que
A Fig. 6-32 mostra três caixotes sendo empurrados sobre um piso de concreto por uma força horizontal F → de módulo 440N . As massas dos caixotes são m 1 = 30,0k g , m 2 = 10,0k g e m 3 = 20,0k g . O c
Um bloco é empurrado sobre um piso horizontal por uma força constante que é aplicada fazendo um ângulo θ para baixo (Fig. 6-19). A Fig. 6-36 mostra o módulo da aceleração α em função do coeficiente de
Um barco de 1000k g está navegando a 90k m / h quando o motor é desligado. O módulo da força de atrito f → k entre o barco e a água é proporcional à velocidade v do barco: f k = 70 v , onde v está em