Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 96
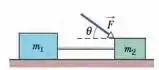
Na Fig. 6-59, o bloco 1 de massa e o bloco 2 de massa estão ligados por um fio de massa desprezível. O bloco 2 é empurrado por uma força de módulo que faz um ângulo com a horizontal. O coeficiente de atrito cinético entre cada bloco e a superfície horizontal é . Qual é a tensão do fio?
Passo 1
Oláaa, querido! Cê está bem? Seguinte, temos dois blocos se movimentando ligados por uma corda tensionada. Eles se movimentam por causa de uma força inclinada aplicada no segundo bloco.
Ele quer a tensão na corda. A aceleração na direção do movimento vai ser a mesma para os dois blocos, porque eles estão ligados pela corda e ela não pode arrebentar ou ficar frouxa.
E como a gente quer achar a força , podemos aplicar a segunda lei de Newton para cada objeto do sistema para encontrar as equações que descrevem o movimento dos blocos.
E se tem segunda lei de Newton na história, precisamos fazer o diagrama do corpo livre para cada objeto. Ficam assim:
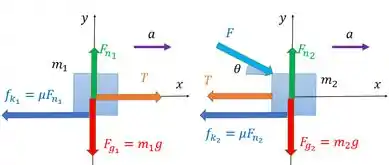
Colocamos o positivo no sentido da aceleração.
Bora lá achar !
Passo 2
A segunda lei de Newton para o bloco no eixo fica:
Sendo que é a a magnitude da aceleração dos blocos. Nessa direção temos a tensão no sentido de positivo.
E temos também a força de atrito cinético nessa direção. Ela tem a expressão , como aponta para negativo, ela fica com sinal de menos. Então o somatório em fica:
Já para o eixo vamos ter que porque não há movimento nessa direção. Nela temos , para cima, então positiva, e temos para baixo, logo negativa. Fica assim:
Já que :
Substituindo (2) em (1):
Passo 3
A segunda lei de Newton para o bloco no eixo fica:
Sendo que é a a magnitude da aceleração dos blocos. Nessa direção temos a tensão no sentido de negativo, e componente de no sentido positivo. Ela vale , porque o ângulo está colado a um eixo paralelo ao eixo .
E temos também a força de atrito cinético nessa direção , como aponta para negativo, ela fica com sinal de menos. Então o somatório em fica:
Já para o eixo vamos ter que porque não há movimento nessa direção. Nela temos , para cima, então positiva, e temos para baixo, logo negativa. E temos a componente de também no sentido para baixo, que é . O somatório fica assim:
Já que e :
Substituindo (5) em (4):
Passo 4
Percebe que a gente tem duas equações e duas incógnitas: e . Então já dá para achar !
Vamos isolar da primeira equação e substituir a segunda:
Isolando :
Substituindo os dados:
Resposta
Tranquilo galera?? Bora resolver mais questões então!!!!!