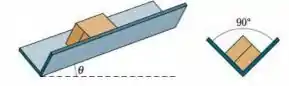
Na Fig. 6-51, um caixote escorrega para baixo em uma vala inclinada cujos lados fazem um ângulo reto. O coeficiente de atrito cinético entre o caixote e a vala é . Qual é a aceleração do caixote em termos de , e ?

Então galera , bora dar uma olhada na ilustração para entendermos melhor o problema. Cada lado da vala exerce uma força normal sobre o caixote. Temos que :

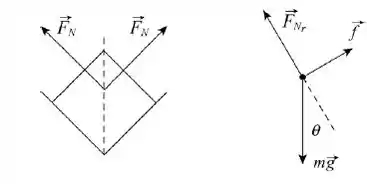
A força resultante tem a direção na reta tracejada. Como as duas forças normais fazem um ângulo de com a reta tracejada, o módulo da força resultante é :

A figura da direita é o diagrama de corpo livre do caixote. é a força normal resultante, é a força da gravidade e é a força de atrito. Como de costume , escolhemos um eixo encosta abaixo e um eixo y da direção de . Aplicando a Segunda Lei de Newton aos eixos e , temos: