Um estudante, enlouquecido pelos exames finais, usa uma força de módulo e ângulo para empurrar um bloco de no teto do quarto (Fig. 6-52). Se o coeficiente de atrito cinético entre o bloco e o teto é , qual é o módulo da aceleração do bloco?
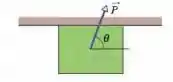
Passo 1
Então pessoal , as forças verticais que agem sobre o bloco são a força normal exercida pelo teto, a força da gravidade e a componente vertical de . Nós sabemos que
como a aceleração da direção vertical é zero,
e, portanto, o módulo da força de atrito cinético é dada por :
Passo 2
Como de costume , escolhendo um eixo para a direita, a Segunda Lei de Newton nos dá :
Fazendo , e , obtemos .
Resposta
De boa pessoal??? Bora resolver mais questões então