Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 31
Um bloco de massa desliza com rapidez constante descendo um plano inclinado de um ângulo com a horizontal. Logo
(a) , (b) , (c) , (d) .
Passo 1
A gente tem um bloco de massa deslizando com velocidade constante em um plano inclinado e queremos descobrir quem é .
Vamos fazer um esqueminha:
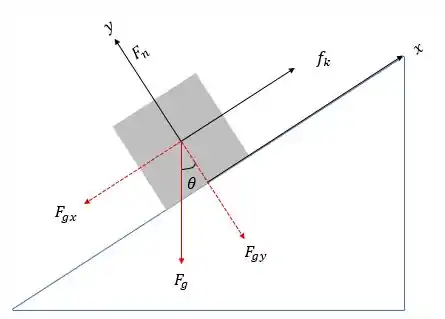
Bem, se o bloco desliza com velocidade constante, então sua aceleração é igual a e com isso a força resultante em , é igual a zero, pois:
Temos que decompor , para isso fazemos:
E:
Agora podemos fazer o somatório das forças:
Em :
Em :
Passo 2
Queremos achar uma expressão para , para isso temos:
Podemos isolar e substituir e que achamos fazendo o somatório de forças:
Logo:
Agora é só olhar nas opções que o problema nos deu e ver qual é igual:
Resposta
Exercícios de Livros Relacionados
Você está sentado no banco do passageiro de um carro que percorre com muita rapidez uma pista circular, horizontal e plana. Sentado, você "sente" uma "força" empurrando-o para fora da pista. Qual é a
Estime a rapidez terminal de uma gota de chuva de tamanho médio e de uma pedra de granizo do tamanho de uma bola de golfe. Dica: Veja os Problemas 26 e 27.
Um bloco de madeira é puxado com velocidade constante por um cordão horizontal sobre uma superfície horizontal, com uma força constante de 20 N. O coeficiente de atrito cinético entre as superfícies é
Estime o tamanho do maior passo que você pode dar estando sobre uma superfície gelada e seca. Isto é, a que distância você pode separar seus pés com segurança, sem escorregar? Seja 0,25 o coeficiente
Estime o menor coeficiente de atrito estático entre os pneus de um automóvel e a pista, necessário para perfazer uma curva para a esquerda em uma esquina urbana, onde o limite superior de rapidez em v